The Support Vector Machine is a kind that is a machine-learning model widely employed to solve classification issues. SVM is a linear approach to classification and can only classify binary issues (i.e., that the Y variable is comprised of the same two classes). In this blog article, SVM will be understood through a quick understanding of the math that underlies it.
Understanding SVM Visually
Before we can understand SVM and its applications, let’s look at how a linear model of classification functions if we consider a set of data with the Y variable comprising two categories, one being -1 and the other 1. Below, the -1 data points are displayed with Red Squares, while the 1 data points are displayed with Blue Circles.
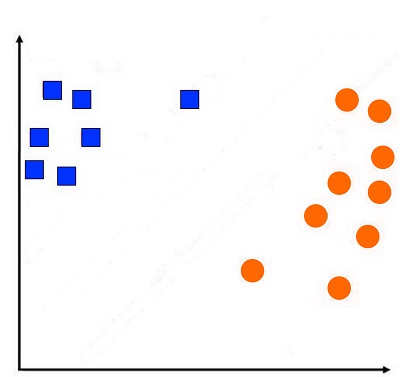
A linear classification technique employs the decimal boundary (a line in the case of two dimensions or a hyperplane in the case of a multi-dimensional issue) to categorize the data points.
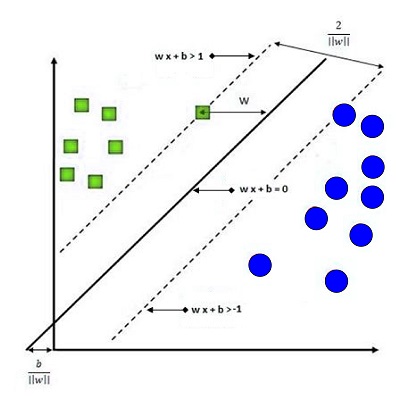
The equation for each hyperplane is wx + B = 0
To properly classify the data, let’s take, for example, input xi. It should provide us with the value of w xi + B > 0. If Yi = 1. (i.e., the equation must provide us with a number greater than 0 if the label has a positive value (1)). The hyperplane equation, with an input of xi, will give us an equation of w xi + B zero if Yi is -1 (i.e., the equation will provide us with a value less than 0 when the label appears to be negative(-1)).
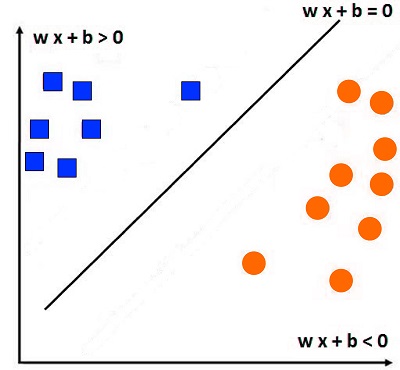
In all of these equations, what we are referring to is that if the number calculated by the formula is lower than zero, The datapoint is likely to be beneath the hyperplane (and will be presented as a red square); however, if the value is higher than 0, the point will be located higher than the hyperplane (and will be classified as a blue square). This information can be summarized in an equation like:
Yi (w xi + b) > 0
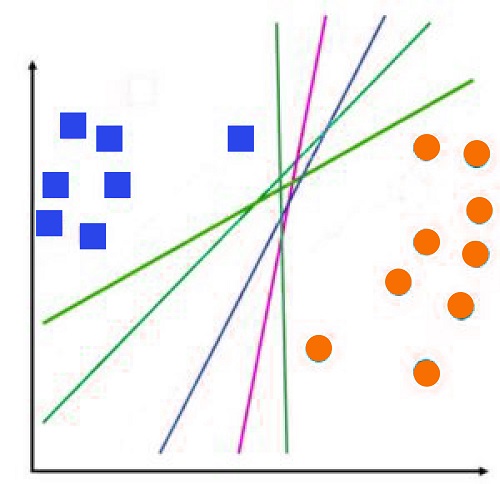
Then we return to SVM. As we said, many lines are drawn to distinguish the two classes; however, the question is, which line is the best to divide the data? Unlike other linear techniques, lines of greatest fit are utilized in linear regression, which can be determined with an Ordinary Least Square Error. SVM employs a different approach to arrive at its decision-making boundary. Instead of simply forming hyperplanes to divide all the information points, it utilizes margins to determine which boundary be drawn.
It is important to understand this concept intuitively. Instead of using all information points available, SVM tries to maximize the distance between these two kinds of information points by increasing their margin, where the margin is defined as the distance between the hyperplane and the point closest near the hyperplane.
This way, we can increase the distance between two data points, allowing for better generalization. The following figure employs a straight decision line (dotted line). Interestingly, using this line can cause a point to be classified as a circle when it was actually a square.
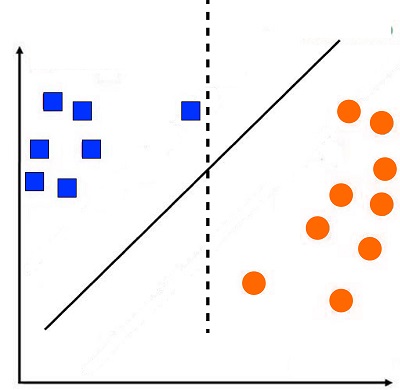
But, if we apply a decision line derived from SVM that is based on the distance between two nearest data points belonging to distinct categories (solid line), the data point is properly classified.
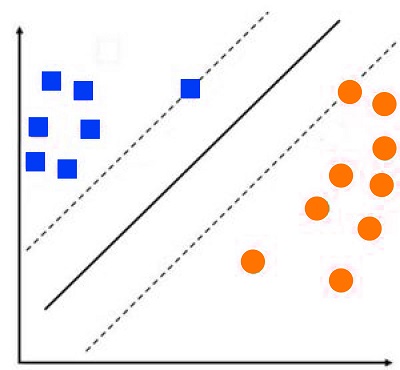
The method of using margin in order to create the decision line is referred to by the name of Maximizing Margin Linear Classifier. In the example above, we can create the decision line making use of SVM, which in this case employs two vectors of support. The support vectors are data points upon the basis of which the margins are constructed. In our case, two data points are used to increase the distance between these two types of points.
This is how we can come up with an option to split the data so that the two support vectors are as far off the line as they can be and thus maximize the margin.
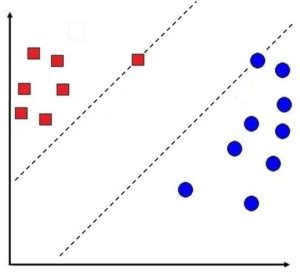
In the end, we could say that to construct a decision line, using SVM, we could create two lines of margin over the data points from two classes that are closest to one another and draw a decision line between these margin lines.
Decision Line Mathematically
Making the decision lines can be more complex than the concepts presented so far because SVM is an optimization problem with constrained constraints. The restriction is that the line has to categorize the data points correctly, so if there is no data, it should be below the decision line, and if it’s a 1, it should be over the line of decision. But, we want to improve the model by increasing the distance between data points closest to this decision line.
To comprehend our constraint mathematically, we’ll write the previously mentioned equations regarding SVM.
The hyperplane equation is the same: w the equation x + b = 0.
But instead of saying that, for the value of xi, we say that w xi + b is greater than 0 when Yi = 1, we can claim that wxi + b > 1 when Yi is1.
Similarly, w xi + b < -1 if Yi = -1 . To simplify the equation, we can create an equation that reads:
Yi (w xi + B) > 1.
This equation will become our constraint. Then SVM will attempt to improve by increasing the margins while taking into consideration the constraints of accurately classifying the data points.
Mathematically, the optimization problems come in determining the edge by selecting arbitrary elements of an object to form the left margin and then adding a normal vector to it in order to get to the opposite margin, then taking the length, i.e., the length of the vector and forming the decision line which is half of the distance of the added vector.
As stated above, We begin by creating the margin-left.
Let’s suppose we have a data point with this amount that is in line with the equation that is: w xi + b + 1 = 0.
We can add an ordinary vector to it ( cw ) which means that the equation changes to the following: (xi + cw) + 1 = 0
Here, the c is the vector being added to determine the margin to follow.
In this case, the value of CW is important because If it is higher, then it will result in a larger margin.
Then we apply the two formulas ( w * xi + b = 0 , and the equation w (xi + cw) + 1 + b = 0.) and create an entirely new equation:
W XI + B + 1. = wxi + the cw + the b + 1
We then can cancel out the w xi and the b from both sides and create a different equation:
W xi + b + 1. = wxi + the cw + the b + 1
WCW = 2
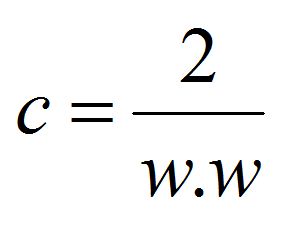
This is the margin, and we need to maximize this. This is the same as reciprocal, which reduces the-
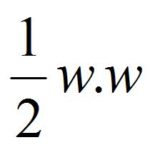
This was the part we optimized.
To put the optimization and constraint together, we arrive at the equation:
Limit (maximize your margin) with the limitation on Yi (w xi + b) greater than 1. (accurately classify all data).
For this, manually, we must find the values for (vector of coefficients) and w (vector of coefficients) and the value of b (bias/constant), but this is something we’ll leave to the software.
Hard Margins V/s Soft Margins
While working on an SVM model, the main problem is determining the ideal equilibrium between the constraints and optimization because as we ease the constraint, we can optimize the model, but loosening the constraint too much could result in the creation of a weak model.
First, let’s intuitively understand this.
For instance, we have a database that contains data points as seen below:
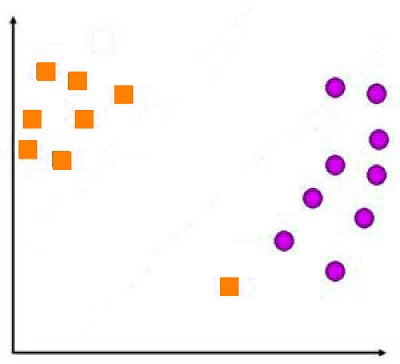
If we design an ad hoc decision line in which the constraint isn’t loosening (margins aren’t reduced), then we’ll have a decision line that includes all data points that will be correctly classified. The decision line generated by SVM will appear like this:
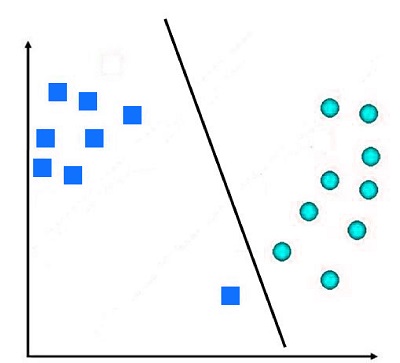
This is a method of hard Margin since there is no chance of making any mistakes. Boser invented this method in 1992. It can be used only if all the data is classified linearly.
But, we can observe that, as a result, we can create an extremely narrow margin. If we allow for the misclassification of a single data point, we could come up with a larger margin than the one we currently have. This is called The Soft Margin, where the constraint is relaxed, and there is the possibility of making mistakes. In this scenario, the decision line could appear to be something like this:
This allows us to maximize the margin by allowing some degree of error to occur. Soft Margins are employed to deal with data that are not able to be separated linearly, and by allowing for some errors to occur, we can maximize the margins. Soft margins were created through Vapnik at the time of 1995. The advantage or pros of this technique is that it assists in creating an effective model in generalization, and it also helps to reduce the possibility of overfitting.
But making the margins too soft can cause the SVM model to underfit. The flexibility to choose the margins’ softness is managed via C. C, the loss function multiplier. The loss function serves as a method to penalize incorrect classifications. We have figured out the optimization equation that, in the equation below, is known as a regularizer. We will then add the loss function (hinge loss function) to it, whose effects can be controlled using an increaser ( C ).
Thus, the higher C’s value C, the more severe we will penalize the model for making errors. This is why C serves as a tuning knob that allows users to manage any overfitting that occurs in the SVM Model. A higher positive value for C will cause the model to have a strict margin.
Combining the regularizer with the C multiplier and the loss function, we obtain an objective function that is
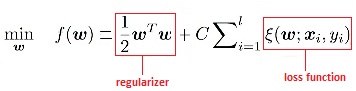
(In SVM, the loss function is called hinge loss. It is written as (1 – Yi (xi, (xi,)). However, this blog post won’t discuss the details of the function).
In order to comprehend how to interpret the equation above in a different way, it is possible to declare that the aim for SVM is optimizing the function that is intended, and the way to do this is to minimize the function of loss. So, as users, we must take care of the C multiplier that can be identified by employing techniques like grid search, which is accompanied by cross-validation.
Kernel Trick
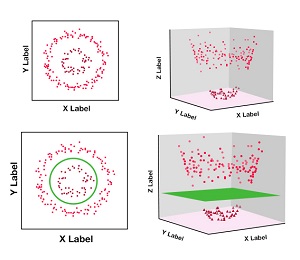
Let’s say we have data that cannot be separable in linear terms, and therefore using a soft margin would not work because it would result in making a mistake in the classification of a lot of data.
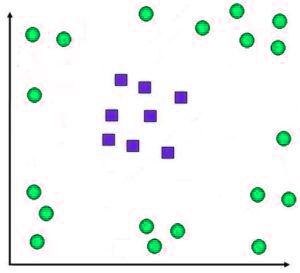
In this case, we will use the non-linear method of classification, which employs SVM using kernel tricks.
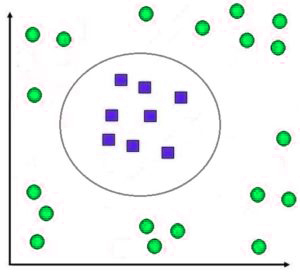
Vladimir Vapnik developed the method in 1992, where the data set was transformed into a bigger dimension, where linear classification could be made.
This is because each dot of input data points is mapped onto the feature space using transformation with the aid of the kernel function.
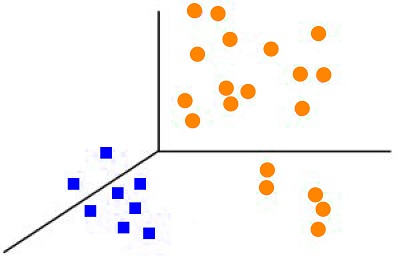
There are numerous ways to accomplish such transformations like Linear Polynomial Sigmoid, Gaussian (Radial Basis Function), String Histogram Intersection, and so on. The RBF function is the most frequently utilized. It contains two common hyper-parameters that can be adjusted, C and Gamma, where C is the multiplier of the loss function (discussed in the previous paragraph). At the same time, Gamma can be used to adjust the kernel. It can also be used to manage the model’s complexity level. Greater gamma values make the model more complicated, and a low value can cause the model not to fit. Both of these parameters can be determined using grid searches.
This is why the kernel trick is a fantastic method of segregating data that cannot be classified using soft and hard margins.
Support Vector Machines is an extremely useful method that is great in two-class classification issues, particularly for situations where there are large and the data is very small. However, its weaknesses are evident when faced with the need for multiclass classification. Additionally, SVM is sensitive to noise and is less reliable as you increase the volume of data. Furthermore, the choice of kernel plays a significant aspect when using the non-linear method. It’s common to evaluate different models using different kernels. All this results in SVM extremely computationally demanding. However, it is one of the most efficient methods to tackle binary classification issues.
