In this blog post, three mathematical concepts are discussed to assist us in understanding how different Inferential Statistics work. They include Standard Error, Standard Error of Mean as well as The Central Limit Theorem. Each one is a brief discussion.
Standard Error
Standard Error means the deviation from the mean and, in a sense, is comparable with Standard Deviation as both are measures of spread, but with one major difference. Standard Error is used as an instrument to measure the difference between various sampling methods and also the mean of the entire population (actual mean), so it is a statistical measure, whereas Standard Deviation is a parameter because the information from the population is included. Therefore, it is possible to conclude that Standard Error is nothing more than an average deviation from the distribution of samples.
According to the Formula, Standard Error is what you will see in the denominator in calculating different kinds Of Inferential Statistics. Standard Error is used as an element in formulas for inferential statistics is because Standard Error tells us about the degree of variation expected when drawing another sample similar to the population.
Standard Error of Mean
It is crucial to remember it is true that Standard Errors exist in every kind of statistical data. We are primarily concerned with the Standard Error of Mean. However, before that, there are certain terms that are important to know to be aware of
- Sampling The Distribution If we take 200 random samples and then compute the means for each one, then the 200 mean would be the distribution that will be known as Sampling The Distribution of Mean.
- Expected Value of Mean: It refers to the average of the distribution mentioned above, also referred to as the mean of the population.
- Standard Error – The Standard Deviation of the Sample Distribution.
Standard Error of the Mean is the term used to describe the average distance between the expected value and the mean of the population in addition to the mean of an individual sample. The Standard Error of Mean allows us to determine the extent to which our anticipated mean is in line with the actual mean of the population, i.e., how much of the real mean I think my estimate represents.
The Standard Error of the Mean is determined by dividing the sample’s standard deviation, or the estimation for the Standard Deviation (i.e., what is the average deviation for an entire sample ) by an estimate of square roots for the size of the sample (for instance, the number of people who are included in this sample).
The formula for standard error of Mean the following:
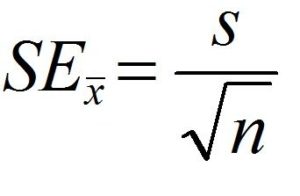
The formula above should be applied in cases where the standard deviation in the population is unknown. We use what is known as the standard deviation (Standard Error) and divided by the square root of the total number of samples. When you know the average deviation for the sample, employ the formula below, where we take an estimate of standard deviation and then split it into the square root for the entire amount of samples.
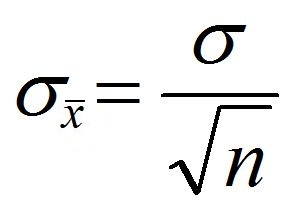
Differentiation Between Standard Error and Standard mean
If you’re trying to be aware of all these concepts for the first time, the jargon of statistics can make you confused, especially words like Standard Error and Standard Error of mean that sound extremely alike to one another.
In simpler terms, Standard Error, like Standard Deviation, can help us understand the dispersion or spread of our data within the sample distribution or the sampling Distribution of the Mean. (Thus, Standard Error represents the normal deviation in the distribution of sampling for the statistic). Standard Error is a term of Statistics used to measure the accuracy of a sample’s representation of the population. In the field of statistics, sample means differ from the real average of a population. This is known as the standard error. “Standard error” or “standard error” is used to describe what is the average deviation for different statistical samples, such as the median or mean. For instance, “standard error of the median “standard error of the mean” is what is the normal deviation in the distributions of means of samples that are taken from a sample. The lower the standard error, the more accurate the representative sample is of the general population. So this Standard Error of the Mean indicates how far from the actual mean of the population. Note that the Standard Error of the Mean value is always less than what is known as the Standard Error. Don’t confuse the words Standard Deviation, Standard Error Standard Deviation in Sample’, etc. The Standard Deviation of the complete population is referred to by the term the s (Sigma), which is determined by taking its square root of variance from each individual data element and the mean of the population by calculating the sum of those numbers and then dividing the sum by the size of the sample and calculating the variance and then taking the square root of the variance.
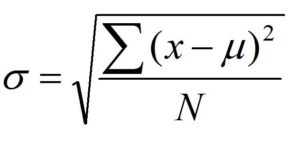
While the term “Standard Deviation of Sample’ or “Standard Error’ refers to the exact identical thing. They have the exact same formula, with the main difference being that it calculates the average using the sample. In the denominator, the size of the sample is subtracted by one. In this case, the Standard Deviation symbol is “s.”
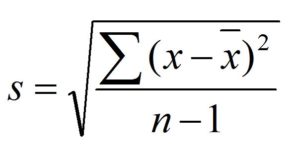
Be aware it is important to remember that the Standard Error of the Mean is just a form of Standard Error. It is used for any kind of statistic like Correlations, Regression, T-Test, etc. there are different types of Standard Errors that can be employed in the denominator of their formulas.
Central Limit Theorem
There is a question to be asked why do we believe an average sample’s distribution to be identical to the average of the population from whom it was drawn. This is believed to be due to the Central Limit Theorem, which states that if we plot the mean of all data points on a graph, the graph will follow the Normal Distribution regardless of the population’s distribution. This is the opposite of what we would expect in which, even if the population itself is non-normally distributed, then the distribution of samples will be normalized.
In addition, it says that the average of all samples will be convergent or close to the average of the population. As an example, there are 100,000 residents in an urban area. We collect 40 samples, each comprising 40 individuals, to determine the town’s median income and draw the mean for each sample. Based on Central Limit Theorem, the distribution from this data will be normal, and the average derived from such a distribution will be approximately the same as the mean of the entire population (average income of people in this city).
Role of Sample Size
It is vital to understand it is important to note that Central Limit Theorem is applicable when it is huge with a minimum size of 30. This is a reference to the Standard error of Mean, where the sample size is a significant factor. The larger sample size and more precise estimate of the sample mean is the parametric mean—consequently, the larger the size of samples, the lower the Standard Error. If the standard deviation of the sample is very high and the sample size is large, more will be the presumed variation of scores in the population, which in turn means that greater is the Standard Error for the mean.
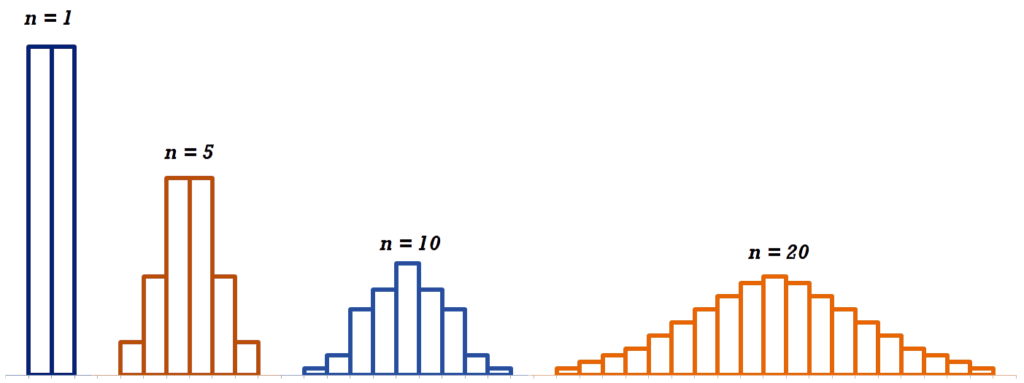
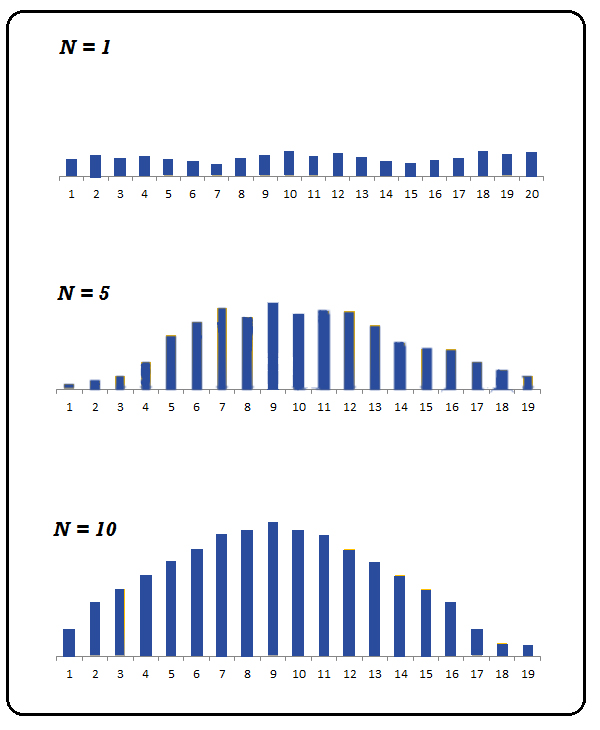
The Sample Error is therefore extremely essential in Inferential statistics, as one or another type of sample error is utilized in Inferential Statistics like T-tests, ANOVA, Regression, etc. The use of Sample Error occurs when we study the sample and wish to draw conclusions. In drawing any conclusions, based on what we see in the sample, we want to know what proportion of it is actually present in the wider population. Since we must guess the population’s meaning for doing this, Sample Error comes into the picture. Additionally, Central Limit Theorem makes it possible to draw our distribution in a normal form, which helps draw the population’s probabilities from the sample. The same will be discussed in the next blog.
