Measures of Central Tendency is another majorly utilized Descriptive statistic. Measures of Central Tendency are used to summarise the data into the use of a single number that represents what is considered to be the center of the distribution. There are three measures of Central Tendency. Mode median, Mode, and Mean.
Mean
Mean refers to an arithmetic median of a score distribution, often referred to as the arithmetic mean. It is a quick summary of the distribution. However, it doesn’t reveal anything about the extent of the distribution. Mean can be determined by using the total of all observations in a data set and then dividing it in half by the number of observations i.e.
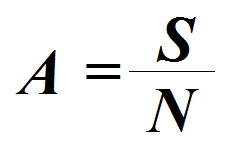
where,
S = the sum of observations within the set of observations that are of interest
N = the number of observations
For instance, there is a dataset that has 5 (five) values
96 ,94, 92, 87, 81
We can determine the mean of this data by adding all values(S=450) and then dividing this by the total number of observations (N=10).
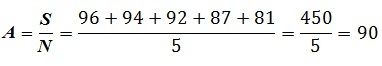
The arithmetic mean of this set of data is 90.
There are advantages and disadvantages of using the mean. Although the mean provides the quickest overview of a data set and can be utilized to analyze continuous and discrete data sets, it can’t be used to analyze qualitative data (Categorical variables). Additionally, the mean is extremely susceptible to extreme values and could yield a highly biased conclusion, especially if there are extreme values in the data. Additionally, the distribution’s form may impact the mean’s outcomes, particularly when the distribution is biased in a way that the mean could give false results. The mean is also unable to explain the variance of scores (variance) and the number of scores near the mean.
The difference between a Parameter & a Statistic was explained in the intro of this section.
If the mean is calculated using an aggregate of data, the mean is a variable represented by the symbol m. Still, if the mean is calculated using an individual sample subset, i.e., from a sample, then the calculated mean will be a statistical figure denoted using the symbol “x. So the formula to calculate the population mean is
m = ( S Xi ) / N
and the formula to calculate Sample Mean will be
x= ( S xi ) / n
in which x represents the mean of the test
M is the word used to describe the word used by the populace,
S is “the amount of”
The X can be described as an individual number within the distribution of the population.
“x” can be described as an individual number within the sampling distribution.
N represents the total score within the test.
N denotes the total number of scores in the population.
Median
The median of a particular dataset can be determined when the data in the data are presented in ascending or decreasing order. The middle value or the value at the 50th percentile of the data’s distribution is referred to as its Median. The Median divides the data into two equal portions with 50% of the observations on either side.
In the following example, we have 11 values, and the moment they’re sorted by the smallest to the largest, the value between them is the median (in green).
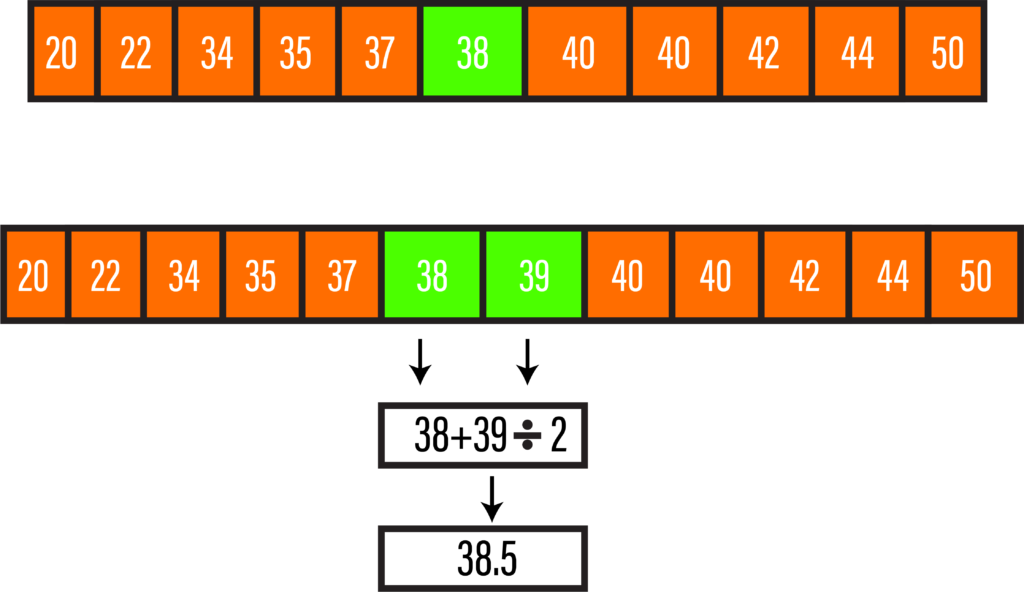
If the value is even, we need to calculate the mean by equalizing the two middle values.
There are a few advantages of median over mean. The main advantages are that the median is not affected by outliers or when the data distribution is tilted. Median, however, can’t be used to analyze certain types of categorical data like Nominal Categorical Data as they cannot be classified based on their weights because the values don’t carry any weight and therefore cannot be placed in logical order.
The Median and the Mean are indicators of Central Tendency, which are the most valuable statistics since they give information about the entire distribution in one number; however, it is crucial to remember that they overlook an abundance of data about the distribution, making it possible to abuse them and to make broad generalizations based on the mean or median.
Mode
The measure of mode can be determined by calculating the frequency of scores within a distribution. It is one of the less utilized Measures of Central Tendency because it cannot offer much data.
For instance, there is data showing the number of vehicles a household owns. In the example below, we looked at 20 houses, and the most frequent mode is the one that is repeated the most frequently.
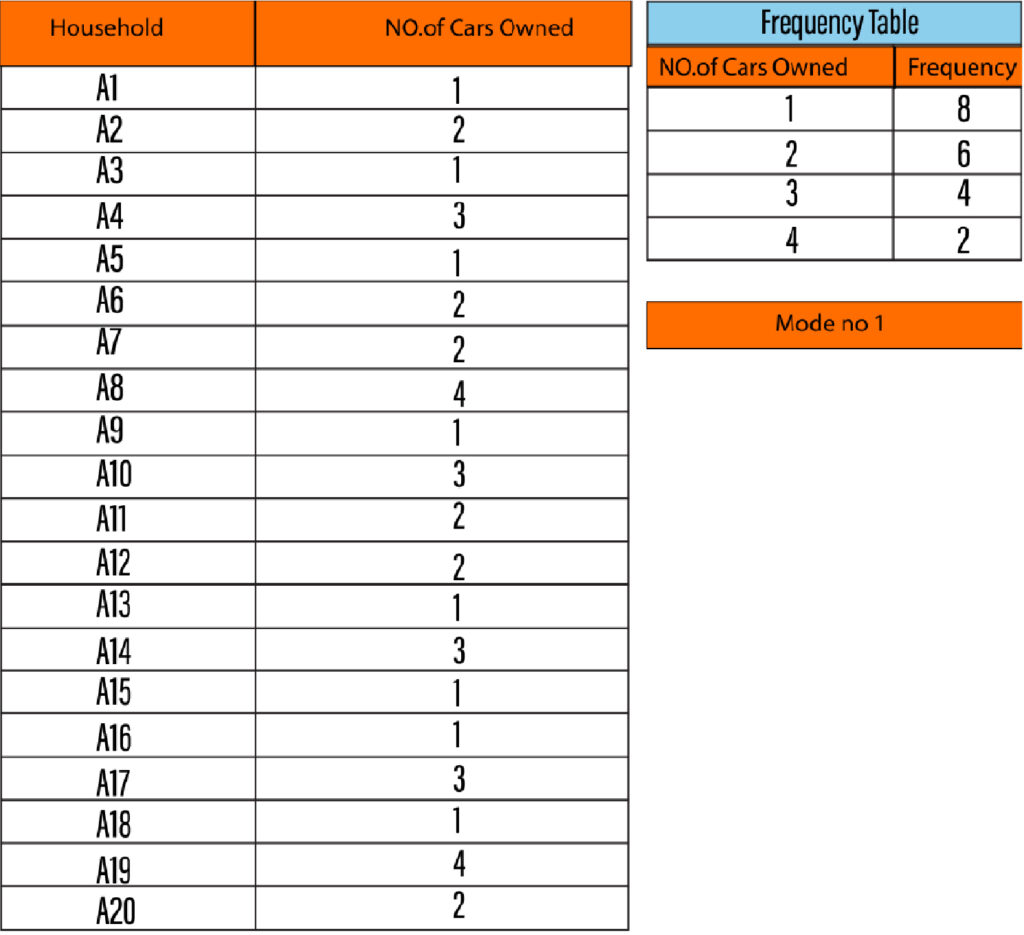
The mode has an advantage over mean or median in the sense that it can be used for both numerical & categorical data but suffers when there are no repetitions in the values in the data set (Continuous Numerical Data) or if there is more than one mode in a distribution(Bi-Modal or Multi-Modal Distributions). In these circumstances, the descriptive powers of the mode are diminished.
Outliers and Measures of Central Tendency
In all Three Measures that comprise Central Tendency, it is stated that they could or might not be susceptible to outliers. We will explore this further by providing examples of how to Mean, Median, and Mode could or might not be affected by Outliers.
Outliers and Mean
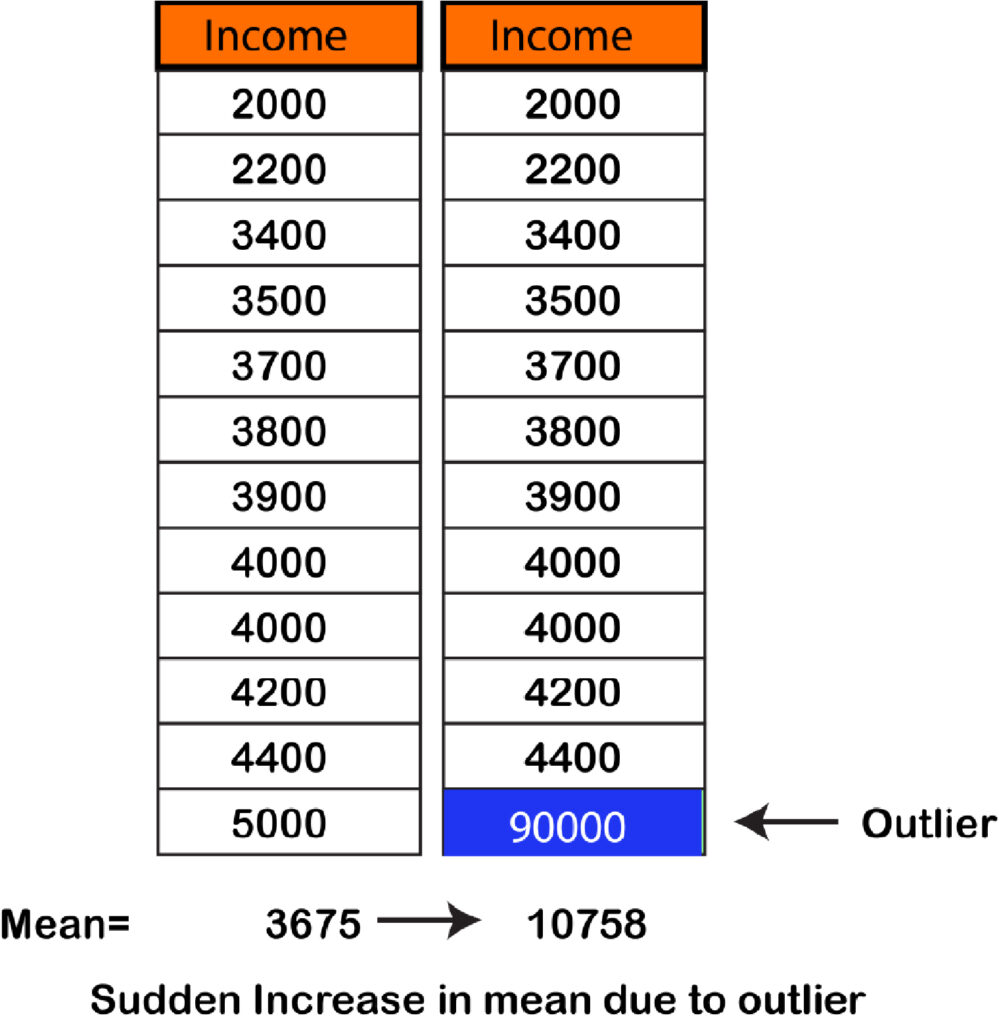
This is an example of the way that because of one non-proportional amount, the median is affected. So if in a set of data, the values are excessively large or small compared to all the other values, this could result in the mean being off.
Outliers and Median
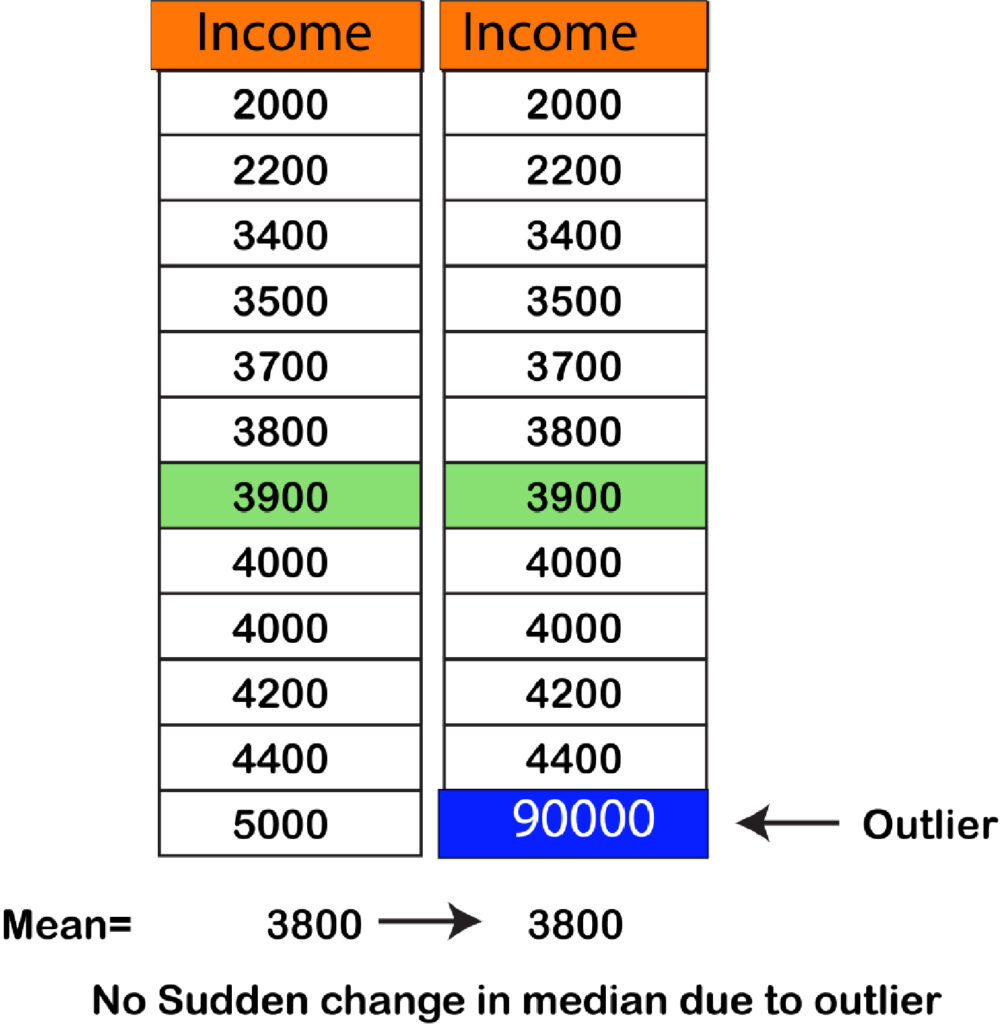
It is evident that the median does not change due to the outlier since after the information is processed, the outlier is either at first (if it is tiny with regard to weight) or at the final (if the weight of the outlier is too high) and the middle value is left.
Outliers and Mode
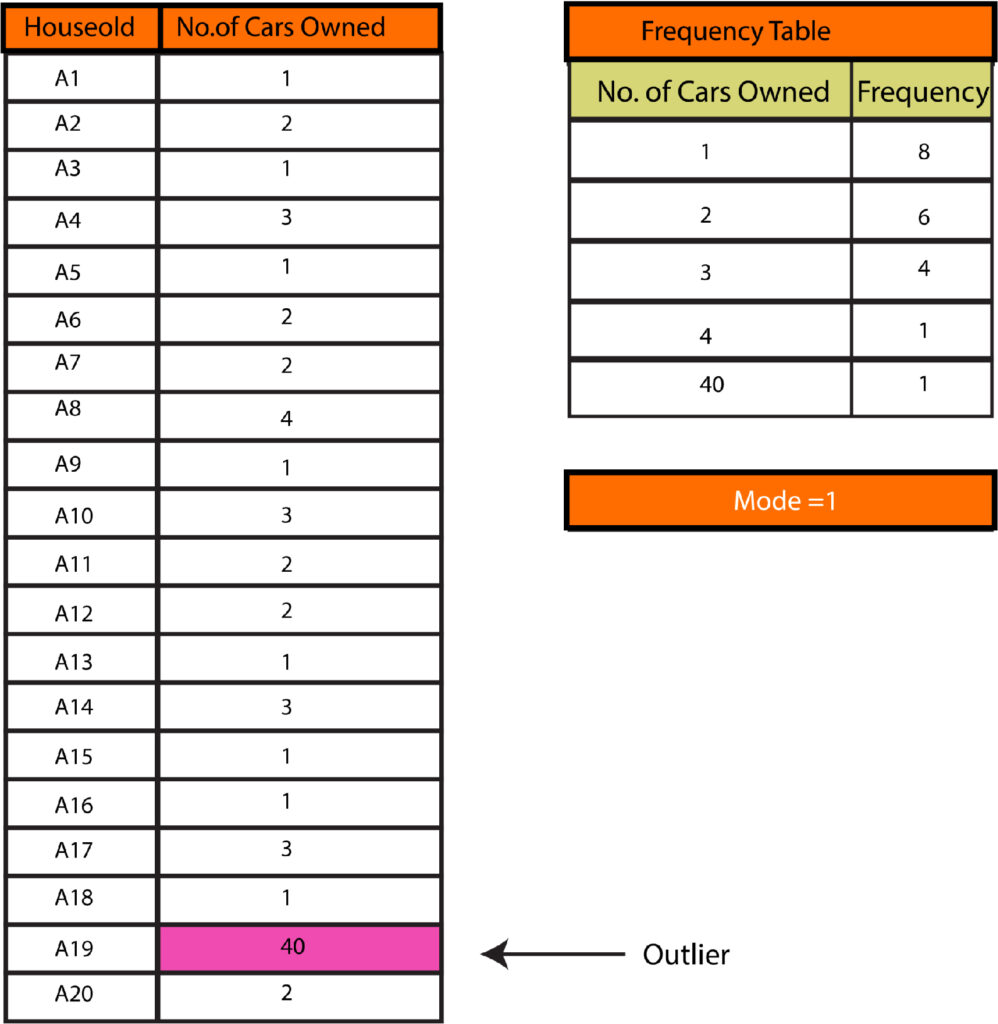
We also add an outlier to the previous examples for mode and discover that mode does not suffer from outliers.
Thus, among all Measures from Central Tendency, the mean is the most vulnerable to outliers, whereas other measures are less vulnerable to outliers.
Therefore, Measures of Central Tendency help us to understand our data by giving us a single value. A variety of measures of Central Tendency can be used in conjunction with using Mean to describe numerical values and the Mode used for categorical data. But they do not clarify the data’s distribution; for instance, the variable with a value of 6 times 6 is likely to have a median value of 6, and a value of 2, 3, 4, 6, 8, or 13 would also be a mean of 6. It is, therefore, crucial to know the distribution of data. This is why we need Measures of Variability that help us determine the distribution of the data.
