Statistics can be broken down into Descriptive Statistics and Inferential Statistics. In this chapter, we will discuss the latter.
Descriptive Statistics describes the data, but we do not stop forming any significant conclusion and instead remain in the realm of listing the kinds of data we have. However, when using Inferential Statistics, we make conclusions and extend to making predictions. One of the most significant benefits that we can make of Inferential Statistics is that it allows us to compare the mean of two data sets or subsets of data.
This section explains that you will learn about some crucial statistics that serve as a prerequisite to understanding the way inferences are made from the data described. The section is known as “Important Statistical Concepts,” and the concepts in this section must be comprehended prior to investigating the various Inferential Statistics. After that, specific Inferential Statistics like Co-relation, t-Tests Analysis of Variance (under F Tests), and Chi-square are discussed.
The term “regression” has been intentionally removed from this chapter (even though it’s a form of Inferential Statistics, that is only). It is placed under the category “Modeling” since it would be clear the way this inferential statistic can be employed as a model algorithm. However, one can view it as a component of Inferential Statistics only.

IMPORTANT CONCEPTS
Before gaining a deeper understanding of the various statistics that can be utilized to draw conclusions about the data, it’s crucial to know how we can draw inferences about the entire population from the data at the start. This section focuses on a variety of concepts that enable us to decide whether or not to accept an idea are examined. Different terms like significance level, p-value, etc., which are used in the following sections of Inferential StatiAstics, are discussed.
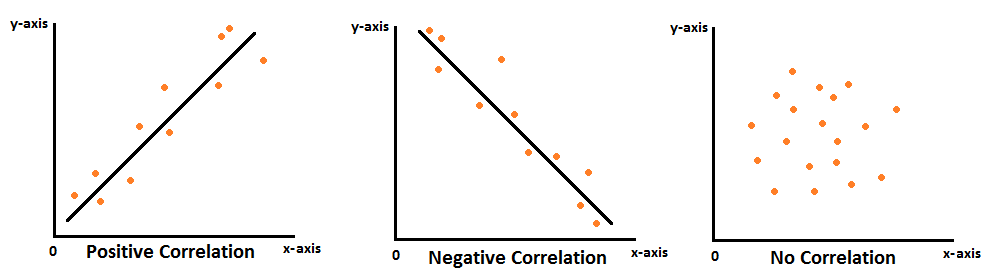
CORRELATION COEFFICIENTS
It is the most fundamental and easy inferential statistics, yet it can also be the most significant one. Correlation Coefficients can be utilized to determine if the numbers of two variables are linked to each other but not. This notion plays a significant part within Linear Regression. In this blog, the main focus is the person’s coefficient of product-moment correlation is explained. It also includes an overview of other correlation methods.
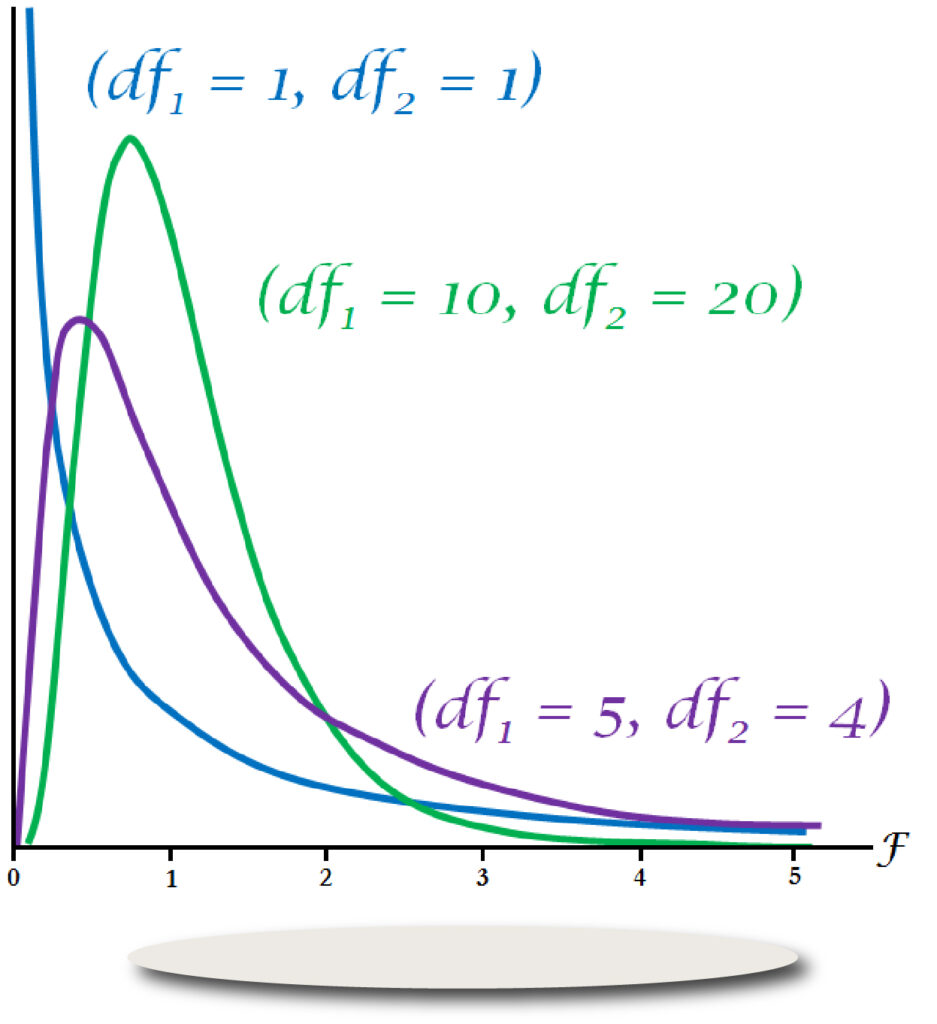
F TESTS
Another statistical test allows you to conduct hypothesis testing, which is to determine whether the two datasets or variables are equivalent to one another or not based on the variance of the two datasets. Many tests in statistical science are referred to as F-tests since they use an F-distribution in the absence of a null hypothesis. F-ratios are calculated to determine whether or not to accept a hypothesis, but in this section, the most well-known F-test include, Analysis of Variance (ANOVA), is examined.
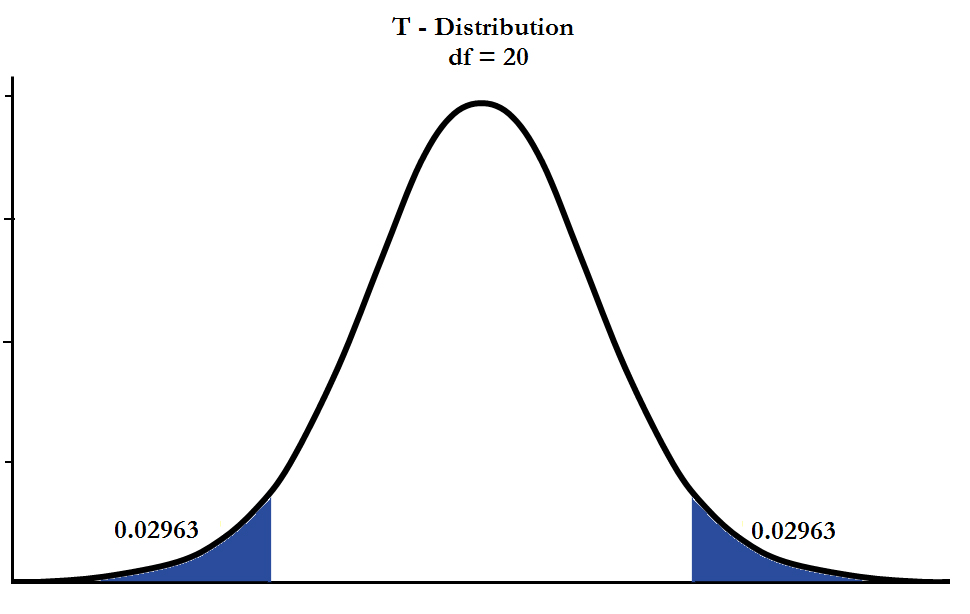
T-TESTS
A test for the hypothesis allows us to evaluate the mean and draw inferences about the means differing from one another or not. Various tests can be used to evaluate the means from two distinct groups, the means from the same person at various times, the mean of a particular group against an assumed value, etc. T-Tests are widely used because they permit us to conduct hypothesis testing even if the sample size isn’t sufficient or the variation of the population isn’t identified.
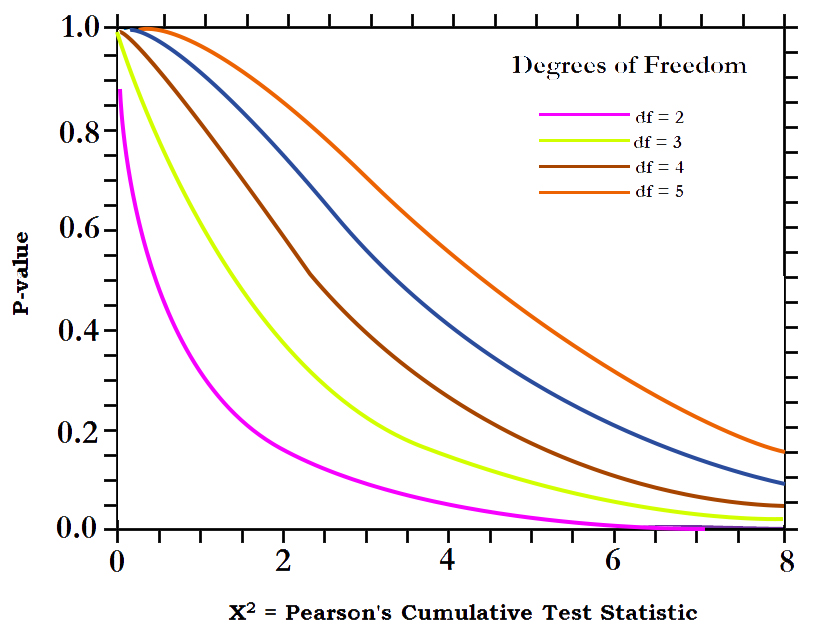
CHI-SQUARE
When you have to evaluate two categorical variables, an statistical hypothesis test is necessary to perform the task, which is exactly what a chi-square test accomplishes. Chi-Square employs frequency tables and the chi-square distribution to assist us in rejecting or accepting the null hypothesis.
