This post will give you an intuitive idea of how Repeated Measures ANOVA works. And, unlike the ANOVA article, we won’t be exploring the formula or its calculations.
Repeated-measures ANOVA v/s Single Way / Factorial ANOVA
ANOVA repeats are similar to Paired P-Test, or the ANOVA. Repeated Measures ANOVA uses the same principle as One-Way Anova. This is where the independent variable’s variance was divided into variances found within and between groups. Repeated Measures ANOVA offers a number of advantages over other methods, including:
*Repeated Measures ANOVA tests related classes and is called such because it examines how the mean of the dependent variable changes over time. So, for example, suppose we have students who are given a math exam at the beginning of the year. We then repeat the exam in the middle and end of the year. In this, the independent variable is the month (essentially, its time), and the dependent variable is the score of students.
*Using Repeated Measures of ANOVA can help control the effects of Covariates. Covariates can be factors such as weather. This allows us to see if the country the children are from can explain the variance in playing time. Children in the USA play more outside than children in Norway, Sweden, and the UK. Repeated Measures ANOVA is a way to control multiple covariates. An ANCOVA- Analysis of Covariance can also be done.
*Unlike Factorial ANOVA, you can have more than one categorical independent variable.
Examples
A few examples will be used to explain Repeated Measures and how they can be applied in certain situations.
First, remember that Repeated Measures ANOVA only works when the data is from the same group of participants. However, the data were collected over different times. This allows us to assess whether or not the changes are meaningful. Repeated Measures ANOVA should have continuous dependent and categorical independent variables.
Example 1.
A group of 50 adults decides to carry out an experiment in which they want to determine if alcohol consumption has any effect on driving reaction time. Let’s take 50 Adults and record the time they take to apply the brakes when directed. After two additional drinks, the same group is asked to measure their reaction time again. Here we now have a second group with two scores on the same dependent variable. Here is the reaction. Now, if we ask our participants to drink two more drinks, they will have three measures of their reaction. One is when they were sober, and two are after they’ve had 2 drinks. The third is after they’ve had 2 more drinks. This makes it a total of four drinks. Repeated Measures ANOVA now shows the change in mean across all three trials. It is statistically significant that the mean shifts over time, making it clear that drinks can increase reaction time. The Alcohol manufacturer objected to our test, stating that alcohol has a greater effect on people who weigh less. Since we haven’t considered weight in our analysis, weight is included as a covariate. This will partially explain the variance in reaction times. After controlling for weight effects, the results were identical. Therefore, weight was not able to explain the variance in people’s reaction times over time. Now, the alcohol manufacturers claim that the response time is dependent on gender. The reaction time of “lightweight” females reacts slower to alcohol than those of “heavier males.” Test this by taking 100 males (100 females) and testing their reaction time after driving with zero, two, and four alcoholic drinks.
“Now I have one dependent variable, reaction time (measured at three time points), one covariate weight (measured at three-time intervals), and one independent variable (gender) in the group. It is important to note that, although it technically is an independent variable (number of drinks), it is not a group or categorical variable. This means that I don’t have three independent categories (the zero-drink category, the two-drink category, and the four-drink category). Instead, I have three dependent (or repeated) measures of the dependent variable, reaction times em>
After controlling the effect on the covariates, we found that there was no difference between interaction time and drink consumption. So reaction time became slower for both males and females.
Example 2.
We would like to find out if students have increased their knowledge from one academic year to the next. Here you can see the time change. An Aptitude Test is created to assess whether there is any change in knowledge. It is given to students at their eighth and seventh academic years. The group consists of 10 students. In the end, there will be two sets of scores. Now, we can calculate the average and variance of these scores.

We will use Repeated Measures ANOVA. This will allow us to determine the sources of these variations. For this purpose, we split the total variance into several pieces.
The first source of Variation
The variance in marks that can cause the most variation is the amount of variance due to student differences. There are two scores for each student. We then calculate and compare the average score with the overall average score. Example: For student A, the average score was 59 (54+64 / 2), and this score can be compared with 68.66 for the overall score. The first source of variation is found in the differences in the average scores for the 10 students.
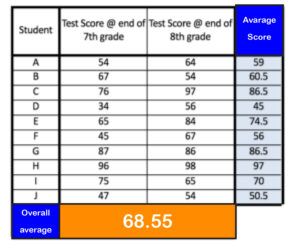
2nd Source of Variation
The second source for variation is the differences in student marks between Time 1 (@ 7th-grade end) and Time 2 (8th-grade end). These scores changes are known as within-subjects effects. We determine the within-subjects impact by comparing individuals’ scores at times 1 and 2. You should note that students’ scores may have changed from Time 1 to Time 2, but their scores at other times were the same. This would cause a canceling effect and no average difference in scores between Time 1 & 2. However, if scores moved up or down without canceling each other, it is possible to attribute some variations to within-subject differences over time. To calculate within-subject variation, we first calculate the average score at each point and then determine the difference between these average scores (and the overall average). It is also possible to see a graph showing how student marks vary from Time 1 through Time 2.


The third source of Variation
Third, interaction comes from the intersubject scores and variances across students. Our sample showed an average increase in scores (65.6 to 72.2), but some students saw a major change, and some students saw a decrease in scores.
Time interaction means that the amount of the test score change from Time 1 and Time 2 is dependent on the student we’re looking at. This is why the Third Source of variation exists.

Calculation F Ratio
To calculate the F statistic for Repeated Measure ANOVA (for Repeated Measure ANOVA), we use the three sources mentioned above and determine if there is a statistically significant difference between the average scores at Time 1 or 2.
“We divide MST (the mean square difference of the time) by the mean square for the subject-by-trial interaction (MSS × T ). The degrees of freedom F is the ratio of the number of trials – 1 (T-1) and (T-1)(S-1), where S represents the number of subjects in the sample).
Using the F Ratio, we can answer questions such as “What is the F Ratio?”.
“How great is the gap between the average scores of Time 1 and Time 2 relative to the average amount variation among subjects in terms of their change over Time 1 to 2?”
“A simple Repeated measure ANOVA can be used to determine whether subjects score differently across multiple data collection points. This is often referred to as an “internal-subjects design.”
Adding an additional Covariate
A covariate can complicate our test. The way we compare averages could be flawed. There was a chance that some students were more intelligent, and their marks rose. Meanwhile, other students had lower marks. The overall increase is because the mark of intelligent students got more marks than other students. ANCOVA (Analysis of Covariance) is used to solve this problem. The covariate of the analysis will be the IQ scores of all students.
When we run the ANCOVA, the data will be divided in 3 ways.
1. Variance can be accounted for using covariate
2. Determine whether the remaining variance is responsible for any change within-subject effects
3. After subtracting the effect of covariates or within-subject effects, there is still variance. This is also known as the error variance.
Adding Independent Group Variable
An independent categorical variable can be used to complicate our test further and may provide us with more insight. An example can illustrate this: Adding a Gender (Two level Independent) variable will help us explain the remaining variance in our dependent variable in two ways.
1. Between-Subject Effect: Let’s say that the average score of boys in Time 1 is 35. For girls, it is 65. However, 52 marks are scored for Boys during Time 2 and 71 for girls. So, the average for boys is lower than that of girls. We conclude that there is a main effect of gender. The main effect is the difference between the cases in the study. This is the so-called between-subject influence.
2. Withinsubjects Effect. The Interaction effect is another source. When we compare the average change of boys and girls between Time 1 and Time 2, we find that the average change for boys has increased more than it did for girls. Time, therefore, plays a significant role in explaining this change. This is called the Within-Subjects Effect.
Thus, the dependent variable (test scores) is affected by a Gender/within-subject interaction.
Repeated Measures ANOVA, like other ANOVA variations, helps us find statistically significant differences between independent variables. But it is time-consuming. The three main types of ANOVA are One Way Factorial, Repeated Measures, and Factorial.
