The Principal Component Analysis is a modeling method that operates in an unsupervised learning setting. In contrast to other techniques discussed in this article, such as Factor Analysis, PCA is not just an unsupervised classification technique but a technique that focuses on removing the greatest variance from characteristics and is therefore used for dimensional reduction. There are a variety of variations of this unsupervised algorithm, including Kernel PCA Linear Discriminant Analysis (LDA) and Independent Component Analysis, and many more.
Overview
Before we get into the specifics and the nitty-gritty of the entire operation of the PCA, we must first have an idea of how it’s functioning. Suppose we have a data set that has various characteristics of a car. They are independent characteristics, and as the dependent variable, we can have the cost of the automobile (a number of variables) or an automobile’s name (a categorical variable). But, the separate features belong to certain groups that closely resemble each other. Some features related to the dimensions of the vehicle, such as dimensions of tires, clearance to the ground and the top of the car’s roof, and the overall dimensions of the car overall vehicle’s height and these aspects can be linked with each other for example, how big the tire could be strongly correlated with the ground clearance, thus not providing any information.
Additionally, other types of features could be present. If the database contains hundreds of features like this which is the case, it can be difficult to discern these kinds of groups since we are unable to see the distinctions from a distance. To determine the groups, for instance, we can create scatter plots that include two factors, weight and height of the vehicle. We find that both variables are strongly correlated with specific cars with a significant correlation (higher height, which in turn means greater weight); however, some vehicles will have a lower correlation (high height, but less weight), but when taken on a general basis, both variables have an increase in correlation. A positive correlation will basically be a sign that they’re indicating the same things, while a negative correlation (for instance, an example of the size of the engine and mileage, when increasing the dimensions of an engine it will be less efficient) could mean that the two variables are comparable but in a different manner.
If we need to analyze a single parameter, it can be done with a simple line, where the data points sit on a line. We can observe the data points which are distinct from each other and the way these data points impact that dependent variable. If we need to determine the connection between two data points, it’s a two-dimensional problem (2-D). It is possible to employ a scatterplot in which both the height and Y (vertical) axis could represent a single variable, while the breadth or X (horizontal) axis could represent another variable. Through it, we can see if these variables are linked to one another or not in the same way; if we were to discover the connection between three variables and then we could use the more sophisticated 3-D plot that includes depth as the third axis that is which is used to represent the third variable. However, it will create problems for us since the analysis of such graphs will be extremely difficult because we’ll need to rotate such graphs in order to discover the connections between the details.
If we are to analyze multiple variables simultaneously and simultaneously, we would need to draw a graph that will include an axis of every feature that is not thought of by the human mind.
For now, we have two choices in the event that we must find connections between 100 variables. Either create thousands of plots in 2-D or create a ridiculous plot that the human brain cannot understand. The answer to this problem is PCA. You can make PCA plots. PCA plot converts relationships or lack of correlations between elements into a two-dimensional graph that clusters the features that are closely related to each other. In our case, there are categories of features that are then classified into ‘Dimensions for car,’ performance Of Car Power of Car,’ and so on.
In other ways, features that don’t offer much information are eliminated, i.e., when there are two elements that have been heavily dependent, we may eliminate one of them. However, when the two features aren’t statistically independent, one characteristic could represent a mixture of different types of information in the same value. To better understand this, we will look at an illustration of image classification in which we employ the blue, green, and red elements of every pixel in an image to categorize the image. The process involves capturing the data using different sensors. Sensors which are the most sensitive to red light are able to capture that color. However, they also capture green and blue light.
Additionally, the sensors most sensitive to green and blue light also show a certain degree of sensitivity toward the red light. Therefore it is true that it is clear that the R, G, and B components are, in essence, interconnected, but it’s easy to see that, even though they’re interconnected, each one is vital and offers details. No feature can be removed in the same way. If we eliminate one of the components, such as the Red part, we remove all information regarding the G and B channels. In order to remove features, we can’t simply eliminate redundant features. We need to transform the feature space so that the actual features that are not correlated are obtained. PCA uses this process to transform data into a different space with new dimensions that are not correlated by linearly mixing the original dimensions, resulting in a distinct set of attributes that is a linear mixture of the input features. The process involves turning the coordinate systems in so that new dimensions become independent and only represent the distinct and independent features of the data. Principal Component Analysis thus reduces larger vector spaces to smaller order by compressing projections of the dimensions. This makes visualization easier, and if data is in three dimensions (for example, R G, B, and R component), PCA converts it into 2 Dimensions by identifying the plane that carries most of the data. The data is then projected onto a new axis and results in a reduction in dimensions. When components’ projections occur, a new axis is constructed to define the relationship. It is referred to as the principal axis. The new features are referred to as principal components. The new dimensions are presented with a score provided by PCA with the higher dimensions that have a high amount of information; however, they offer smaller reductions in the dimensions, and the less dimensional dimensions have a smaller amount of data since the data is located within a closed area, which makes it difficult to distinguish different data samples, however, it reduces the size of the data to the greatest degree.
PCA in Detail
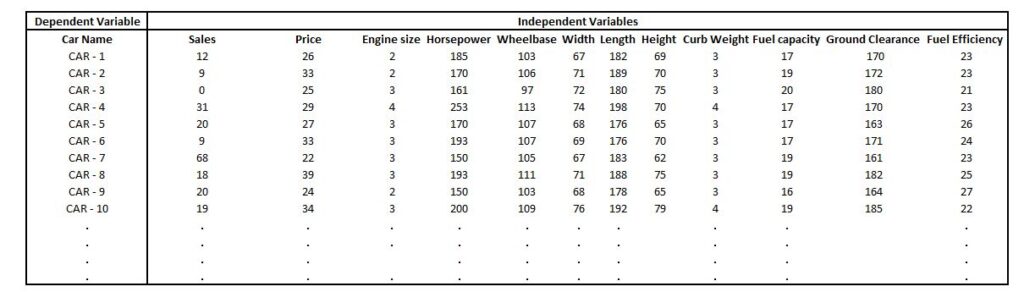
It is first necessary to look at the size of a dataset. For instance, let’s say we have a database in which we have the name of the car as the dependent variable, while the independent variable has diverse details about the car. We wish to shrink the size of the information.
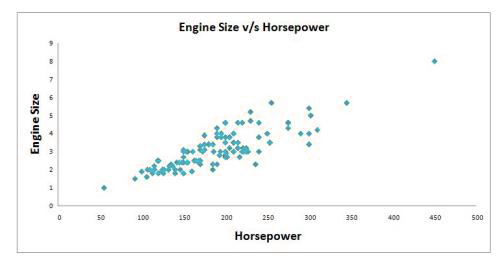
It is possible to create a one-dimensional plot that is nothing more than a line of numbers in which we only have to consider one variable. This is of little use in terms of reducing aspects. You can make a two-dimensional graph that has two axes and show data from two variables. We will use Engine Size in addition to Horsepower and see that they share a positive co-linear relation.
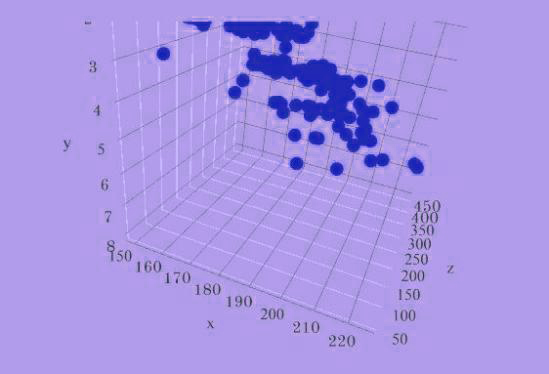
Suppose we need to make an illustration of three variables like length, engine size, and Horsepower. In that case, we will need to design a 3D graph that is needed to be rotated continuously to determine the relationship (which isn’t easy).
Here, the X axis indicates Length, Y represents Engine Size, and Horsepower is shown by the Z axis (Depth).
Suppose we are trying to determine the connections between these three variables. In that case, we’ll have to draw lines parallel to each axis on every data point to determine the point where they all intersect, and we must do this for all data points to draw any conclusion. This fancy graph will not be of any use for us.
To discover relationships between four or more variables, the plot will not be of much help.
As an example, we have hundreds of features. We need to identify those features that are the most essential but to comprehend how PCA helps in the reduction of hundreds of features, let us take the simpler case where there are two features. We need to cut the number of features without sacrificing any aspect, i.e., minimizing the loss of information. If in our 2-D graph (having two variables), there is the most variation in one of the features, while the other feature shows smaller variation. The difference in the data may be described as being from the left and right.
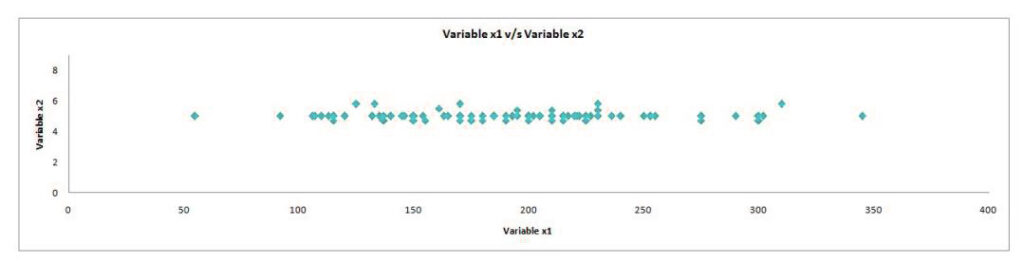
In this instance, only the variable x1 is a variance, while the variable x2 has lower variance. If we take out the tiny variance in the x2 variables, we’ll get a graph that will look like the one below, which could be represented as the 1-Dimensional graph ( the term “number line”). This is how we transformed 2-Dimensional data to 1-Dimensional information without losing any information (hereby information, we refer to as the variance was flattened) because, in both graphs, it is evident that the main variation is left-to-right, i.e., the axis on which the variable x1 is plotted, thus answering our question about what variables are more important. Here, the variable x1 has greater importance.
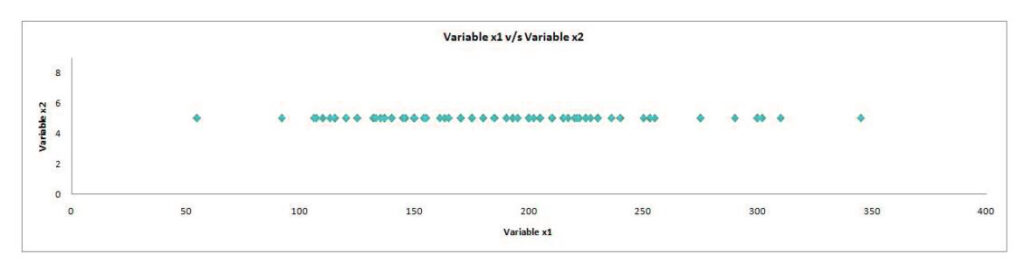
So, every feature is a dimension that adds another; however, each one of these dimensions has distinct variances, which means that certain dimensions are more significant than others. PCA is similar to PCA when it collects information from several dimensions and then flattens it into smaller dimensions (2 Dimensions to display) by figuring out useful ways to flatten the data and focus on the factors that are distinct between the aspects.
Returning to our earlier instance where we discussed Engine Size and Horsepower, we will see that the data points are scattered across the diagonal line. The highest variance in this data can be determined by identifying the two extreme points of this feature (Horsepower). But the dots are distributed over this line, and this variance is due to the variable’s weight, and it is evident that the variance isn’t that big when we look at the two extreme elements of the feature.
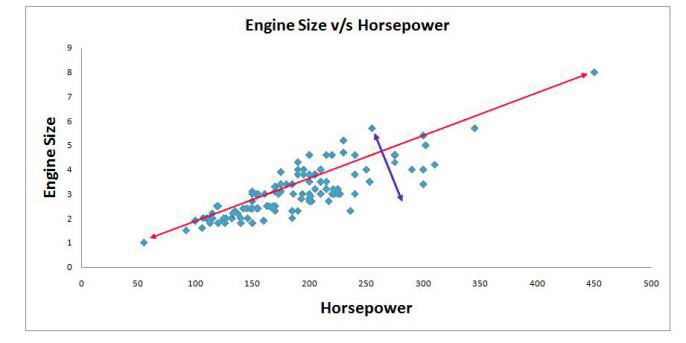
Note: When the extreme value to the right results in the variance increasing in this case, it may be due to the particular data element being an outlier. This is why outliers need to be eliminated, or the data should be standardized to reduce the effects of extreme values.
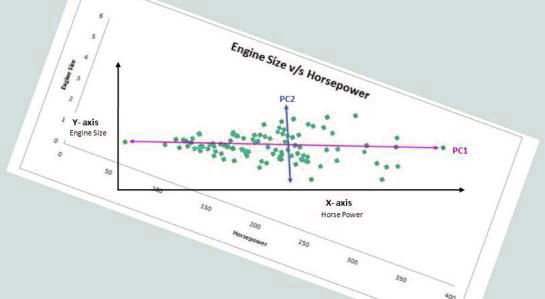
In order to compare this situation to the previous one in which we saw a variance on the axis X and Y. We need to turn the graph until the two lines are parallel to X and Axis. This makes it easier to understand the differences between these lines.
Now we can visualize the variance in terms of left and right, as well as down and up. The two new axes rotate to define the variance in the data. They are referred to as Principal Components. In this case, the principal component is the one that shows the most variation in information (variation across the left from right to left); however, the 2nd one has lesser variations (top-down). Therefore, by comparing the two directions above, we can measure the largest variation based on the numbers.
If we had three variables in this case, we’d be able to see three directions, which generally means that we’d have three principal components with one component for each of the variables. Similar processes will be followed for five, four, and so on, which will have Principal Component 1 as the one that spans in the direction with the highest variation as well as principal Component 2 spanning in the direction with the second-highest variation, and further on. If we have 100 variables, we’ll eventually have 100 principal components. It is important to remember that these axes rank in order of importance, with PC1 being the most significant and PC2 being the most significant, and so on.
In our data, in the event that we have 64 variables and 64 variables, there will be 64 dimensions. In the end, we’ll have 64 Principal Components. However, we would like the information to be compressed to 2 dimensions, thereby using the information from two primary components. Using just two parts, we will lose lots of data that could have helped us identify or predict the desired variable. So, if we employ only two components, which compresses all of our variables into two dimensions, and then project our target variables, our variables will appear very cluttered and may not be properly separated. Still, it becomes easier for us to see graphs. In addition to its loss of information, PCA also comes with some other drawbacks, such as it is prone to reveal linear relationships between different variables, which can be undesirable.
Despite its pros and cons, Principal Component Analysis remains the most well-known and widely utilized Dimensionality Reduction technique. It is recommended to be employed when dealing with extremely large data sets.
