F-test refers to any test that uses a test statistic that includes an F-distribution under an assumption of non-inference. In a sense, F-test is a generic term that covers all tests in statistical analysis which use F-distribution.
So far, the Z test and T tests are being discussed. Each test has its own distribution and formula for calculating its Z Value or the T Value. There are situations that cannot be conducted testing these tests. That’s when the F tests are beneficial. F tests employ F statistics, an equation of variances that is the sum of two. These F Tests use F Distribution. The F ratio is very beneficial and is utilized in a variety of tests (often employed to compare the statistical model). It is one of the well-known applications of this ratio is the comparison of two regression models to determine which one has statistical significance.
So, in contrast to the Z Test / T Test, in which the mean of two sets of data is compared in order to draw inferences for the purposes of the F Test, F statistic can be used to analyze two variances in order to determine whether the means from the different groups differ statistically from one another or not.
There are a variety of tests in which F statistic is utilized; however, the most popular F tests test is called the Analysis of Variance.
Analysis of Variance, more popularly known by its abbreviation ANOVA test, is an additional hypothesis test that differs from T and Z tests (whose calculation is based upon the distribution of data concepts of central tendencies, especially the concept of central tendency, particularly) and is built on variance. ANOVA tests allow us to decide whether or not to accept an unproven hypothesis. ANOVA can be used in cases in which Independent two-sample T-tests may be employed; however, F Test is more adaptable and efficient as compared to the test (ANOVA similar to Z or T-Test is utilized to determine whether the groups involved are similar or not, but as stated above in contrast to T and Z tests ANOVA utilizes variation to determine the differences in mean across the various groups.) In this case, it is the Null Hypothesis can be that there is no distinction between the groups, while the alternative Hypothesis is the opposite. For a better understanding of these situations, let’s look at some scenarios in which ANOVA is used.
- 100 people enrolled in an exercise program for weight loss are offered one of two types of diet (Diet Type 1 or Diet Type II), and you’re looking to determine which one is more beneficial over the other. (Here, we also have the option of using the Independent Two Sample test as the independent variable (Diet Type) includes two different levels (Diet Type 1 and Diet Type II)).
- Students from three schools prepare for their exams in history using strategies for memorizing that were developed by their school teachers. Which method is superior to one?
It is crucial to comprehend the meanings of ‘Dependent variables and Independent variables’ and ‘Groups/Levels.’ In the above-mentioned examples, the dependent variable is dependent on external factors. For instance, in the example, weight is the dependent variable. The independent variable is the kind of Diet, and the various subcategories that comprise the dependent variable are identified as levels or groups.
A variety of ANOVA variations can be used to test different kinds of data. Some of the most commonly used kinds of ANOVA are One Way ANOVA and Factorial ANOVA, Repeated Measures ANOVA, MANOVA, etc. A few of these kinds of ANOVA have been described below.
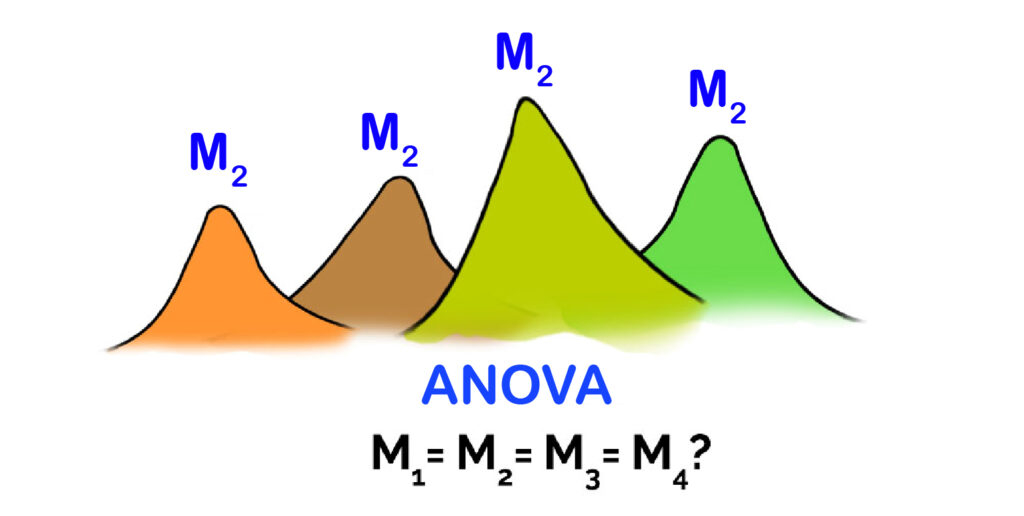
One Way ANOVA
One-way ANOVA can be used to evaluate the mean of two groups of the independent variable to determine if the groups are significantly different.
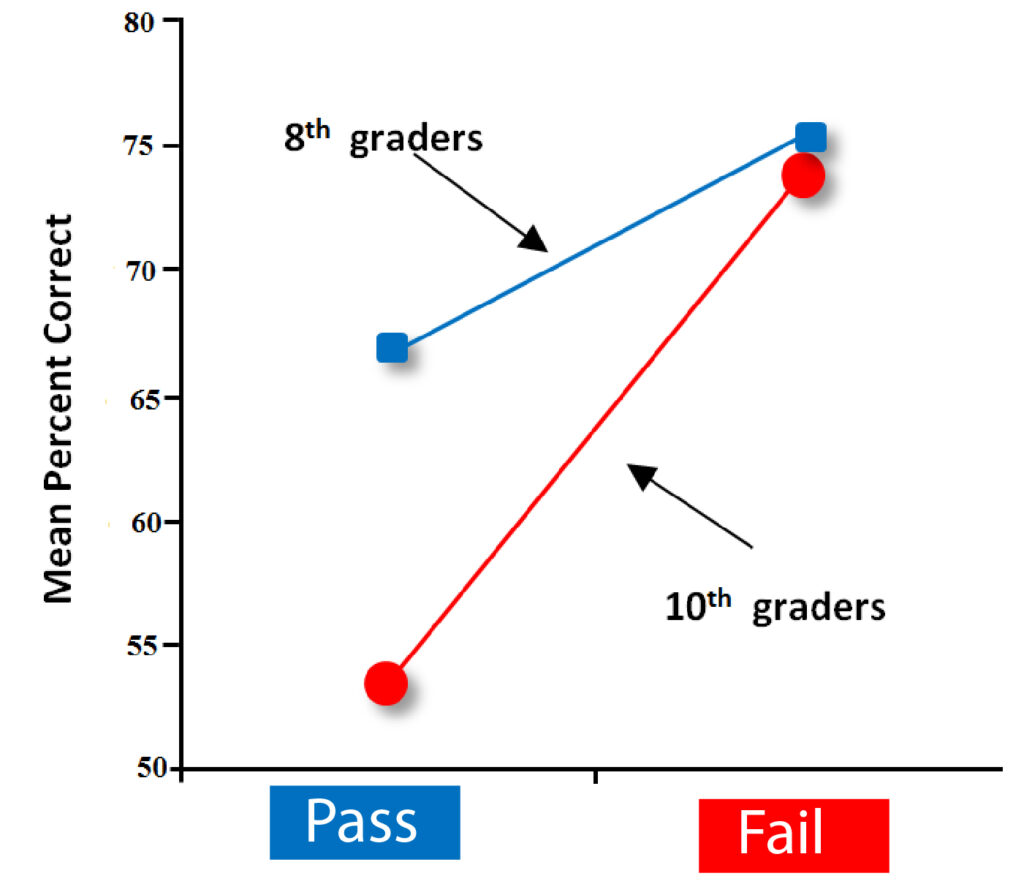
Factorial ANOVA
The concept is an evolution of One Way ANOVA, where groups of dependent variables can be compared to determine the extent to which they are statistically distinct from one another or not.
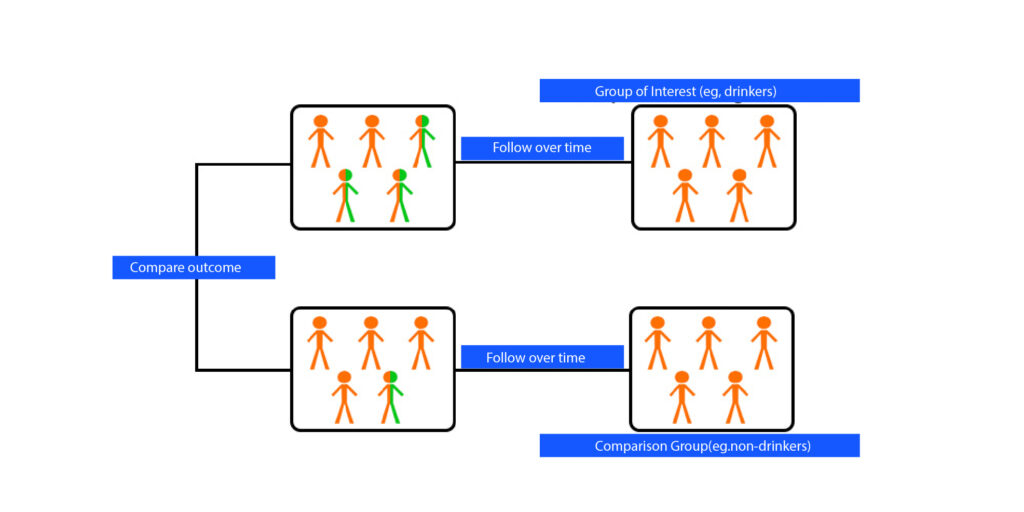
Repeated Measures ANOVA
Repeated Measures ANOVA analyzes groups with similar characteristics. In this case, ANOVA uses it to determine the variance in the mean of the dependent variable for more than two-time intervals.
