Then the blog, the concept of Logistic Regression will be examined. It is strongly recommended to first study Linear Regression as the procedure, and the logistic regression equation is often compared to that of Linear Regression.
Logistic regression is employed for categorical dependent variables. Contrary to Linear Regression, where we must determine the value of the continuous variable in logistic regression, we must determine a categorical variable. Logistic Regression is a method that uses linear methods of classifying the data. It should not confuse with Linear Regression, as linear classification refers to classification done using a linear separator (a line or hyperplane).
Logistic regression is of three kinds: Multinomial, Ordinal, and binary (Binomial). Ordinal Logistic Regression occurs in which the dependent variables are dichotomous, i.e., it has only two categories, whereas with Multinomial Logistic regression, the dependent variable is composed of more than two categories that are ordered or unordered.
Each of these regressions could be either simple, i.e., only having one independent variable, or multiple if there are at least two variables. Binomial Regression works the same way as Ordinal; however, both are defined with respect to one and zero (Binary).
This blog entry will discuss the simple Binomial logistic regression is explained.
Example Dataset
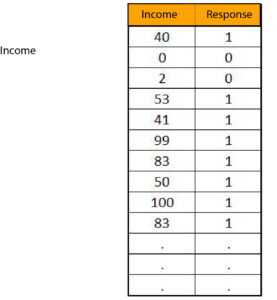
A concrete example can be very helpful in understanding the concept of logistic regression. Imagine we have a data set with an independent variable, ‘Income’ and the dependent variable is, “Response.” This data sets us up about the income of an individual and the response from the credit card company when they apply for a credit card. The independent variable is comprised of continuous (numerical) information while the dependent variable remains discrete with two categories: one representing request accepted’ and 0 representing “request rejected.”
Similar as we performed in Linear Regression, here also we must determine that for a particular amount of x, what would become our value of y? So, we must create a mathematical model that can provide us with a probability of something occurring or not happening for various values of the variable x.
Sample Dataset is showing the first 10 observations.
Different From Linear Regression
The basic principles of regression are the same, and linear regression can’t be a substitute for logistic regression since the primary difference is that the result of y is zero and 1, and it is not continuous.
If we draw the dependent and independent variables on a scatter graph, the most suitable line will not be of any value for us and will not yield any useful results. This is because the linear regression line can be useful in situations where both the independent and dependent variables have a quantitative. Furthermore, binary data (i.e., with just two categories) does not have an average distribution which is a prerequisite to use linear regression.
Furthermore, distributions such as U-shaped distributions are efficiently used in logistic regression.
Additionally, like Linear Regression, Logistic can deal with data in which the relationship between independent and dependent variables is not linear. Logistic regression uses non-linear log transformations based on the predicted odds ratio (more on this later).
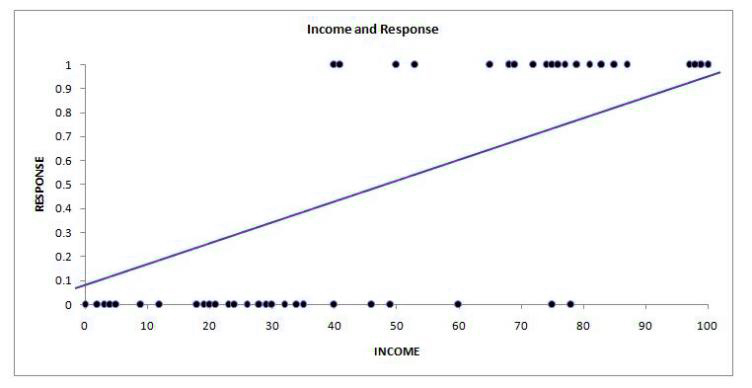
This is the reason logistic regression comes into play, as the model can provide us with the likelihood of an event happening based on the values of the dependent variable. The probabilities are used to predict the value of dependent variables (based upon a cut-off for the probabilities) and may be classified into binary numbers between 1 and zero. Like Linear, Logistic Regression also assists in evaluating the effects of several independent variables on dependent variables (in Multi Logistic Regression).
The drawing of parallels among Linear as well as Logistic Regression
Since a linear function may be fitted to a dependent variable when it is categorical, an inverse link function, also called “the logit function,” is employed in these cases of a binomial distribution. The formula used to calculate the logit function is
P = e a+b x1 + x + b 1 + x
i.e.
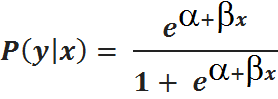
For a quick comparison, we can declare that the probability calculation is made by using the coefficient of Beta-x and Alpha, which can be divided by 1 + Beta-x and Alpha. If you are familiar with the equation for linear regression, Y = a + bx + e, it is possible to declare that a + BX is a factor included in the logit formula, but we also choose an exponent. The method of arriving at the function will be addressed later, but for now, let’s keep drawing parallels between logistic and linear regression.
The Best Fit line of linear regression indicates the value when the independent and dependent variables are in perfect correlation. So, any data points that do not fall on the line are regarded as an error. If our data points fall within the regression line, then scatterplots would appear similar to what’s shown below.
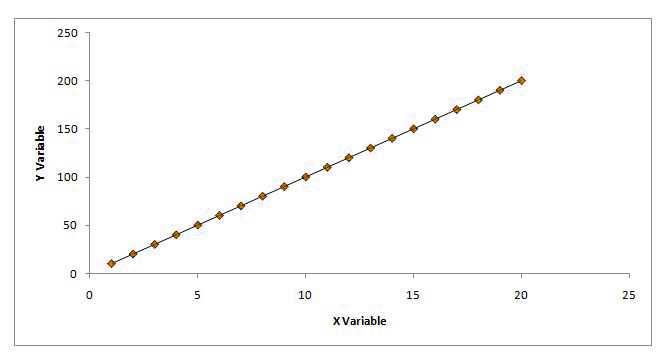
But, it is essential to know the equivalent of this best-fit line of logic in relation to logistic regression.
To illustrate this, a basic example could be utilized. In a data set that we are using, we have “years of schooling in the X variable and “employed” (Yes/No) in the variable dependent (Y variable). We believe that the higher the academic years, the higher would be the likelihood of working. Therefore, as X grows, the chance of the Y number being 1 (Yes, i.e., employed) will rise. In our case, taking 100 individuals who have 10 years of schooling ranging between 0 and 2, then 10 who have years of schooling between 3-4 years old, and the list goes on. Then, we calculate the mean number of people employed (1) within each group, i.e., we calculate the mean score of each dependent variable in every group of independent variables. The mean is simply the chance of finding one. This is why the inverse logit formula (which will be explained in the future) is referred to by the name of the mean. The ideal scenario is similar to the above scenario in that with increasing the years of schooling, the likelihood of being 1(being employed) increases.
A graph or data can look like this:
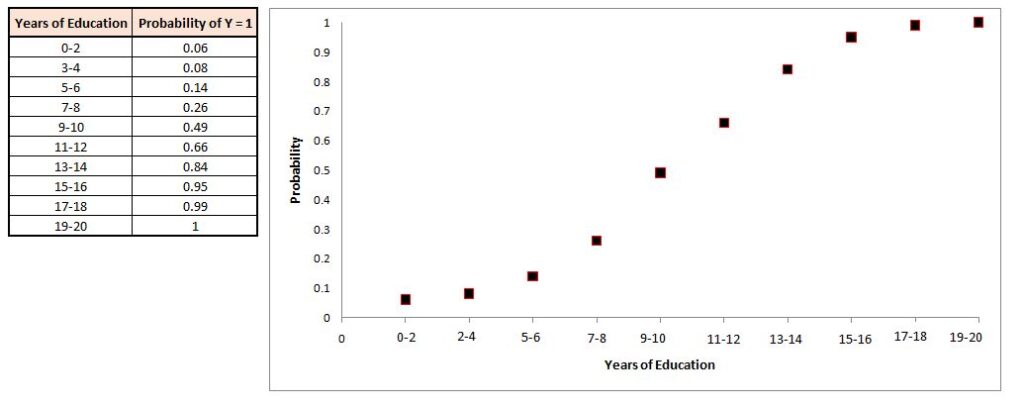
If you pay attention, you can observe how the data points differ from the regression line. The data points here form an S-shaped curve, also known as the sigmoid curvature that is created when we show the average value of y for various values of the x. These average values can be described as anticipated or desired values. This desired curve develops by a change of x likelihood of y=1 is increased proportionally.
A perfect S-curve implies that there is a perfect relationship between the dependent and the independent variables. In the case of logistic, we are hoping for an S-shaped line instead of straight lines, which is what we see when performing linear regression.
This line in the shape of an S has a function that is similar to what the most well-fitting line of the linear regression performed. This function is referred to as”logit.
There are many more similarities to be found between logistic regression and linear regression. They will be discussed when analyzing this function.
Logit Function
To understand the logit function, that is, p = ea + BX / 1 + ea + BX, it is necessary to comprehend 5 equations one after another that can assist us in concluding out of the results. The five equations that are discussed here are:
1) odds = P / (1-P)
2) odds ratio = (P1 / (1 – P1)) / (P0 / (1 – P0))
3.) logit (P) = ln (P / (1-P)
= (a + bx)
4.) Inverse Logit Mean Function = Logit 1(a)
= 1 / 1+ e-z
= ez/ 1 +ez
5) Estimated Regression Equation = p
= ez/ 1 +ez (where z = a + bx)
= + e logit(P)/ 1 + = e logit (P)
= ea +bx / 1 + ea +bx
Odds
To better understand the odds, first, we must review the probability. The probability P is equal to the outcome of interest divided by all possible outcomes.
If, for instance, you flip a coin, then P is 1 / 2. which means the head probability will be 50 percent. If we also roll a dice, the chance of finding the number 1 or 2 is 33%. (2 6 x 1 = 1 3.33 = 0.333).
Odds are probabilities of an event happening divided by the chance of that event never occurring. It could be said that it’s the probability of scenario A occurring divided by the chance of scenario A happening. Thus, the equation for odds would be P (P) / (1-P) which is the likelihood of a specific event happening.
It is important to remember that, in this case, the probability value can’t exceed 1. Returning to our example, The odds of obtaining heads following the flip of a coin will be one (also, you can say that the chances of getting heads will be 1:1). It is calculated using the formula mentioned above.
0.5 / 1 – 0.5 = 0.5 / 0.5 = 1.
The odds of obtaining one or two after the dice roll is 1:2
= 2 / 6-2 (i.e. 0.333 / 1 – 0.333)
= 2 / 4 (i.e. 0.333 / 0.666)
= 1 / 2 (i.e. 0.5)
i.e. 1:2
But why do we need to be able to comprehend the odds? It is important to know the odds in order to be able to comprehend the odds ratio.
Odds Ratio
The name implies that an odds ratio represents the ratio between two chances. The formula used to calculate an odds ratio can be described as:
To comprehend this concept, let’s look at an example in which we have a coin that is loaded, meaning the probabilities of finding heads are greater than the chance of finding tails. For instance, here, the chance of finding heads in this coin is 0.7. Therefore, if we look at this coin in comparison to the normal coin, we will find the odds of finding heads on the coin loaded with heads’.
Thus, the equation here will be –
Therefore, the chance of having heads with loaded coins versus an ordinary good coin stands at 2.33 to 1. i.e., the probability of obtaining heads is 2.33 times more than the odds of getting heads in a normal coin.
What is the reason we need to be aware of the odds-to-return ratio?
It is essential to comprehend the odds ratios because, in logistic regression, the odds ratio will explain the amount of increase or decrease in the chance of obtaining an outcome (of the Y Variable, such as a result is 1.) for each unit of growth in the variable while keeping the other independent variables the same. For example, if you have a dependent variable, diabetes, and an independent variable, weight. And when the odds ratio for the independent variable turns out to be 1.09, that means that every kilogram increase in weight will increase the likelihood of having diabetes by a ratio of 1.09, which is 9 percent. Therefore, if the odds ratio was 2, it could have been that an increase of one pound in weight could increase the chance of having diabetes by the ratio of 2, which is 100 percent. This data plays a crucial function in evaluating the importance of the independent variables as well as their effects on the probabilities of dependent variables.
What does this mean? The odds ratios represent logistic regression coefficients since they provide the same information that linear regression coefficients provided (how much growth in Y is expected for an increase of a unit of the X)?
The answer is not so easy. When we use logistic regression, we find (b) the ratio coefficient (b) for each dependent variable. Still, because of the intricate mathematical translations of these coefficients, they cannot be understood in the same way they were when using linear regression. For instance, if we’ve got an unrelated variable named ‘Income’ and the dependent variable response, which we want to figure out the probabilities of the response being 1 and get a coefficient of 0.013529, that does not mean that a one-time increment in income will raise the probability of the response being 1 by 0.013529 times (1.3 percent). However, understanding the odds ratio is useful since the magnitude of the coefficient ( exp(b) or e B ) is the odds ratio of the independent variable. If we decide to take the slope of the regression exponent of the regression, which in our instance can be 0.013529 and the odds ratio is 1.0136. That means it is 1.0136 times more likely to achieve the Y=1 value for each increment in the variables X. In our example, if the coefficient value was 0.70128 and the odds ratio was 2.016332, then it would be 2.016332, which means it was the dependent value (y) is equal to one and has twice the probability of occurring for an increase of one unit in the dependent variable (2.01 multiplied). If the coefficient was zero or close to 0, it would mean that there was no connection between the dependent and independent variables (the odds ratio would have been one). However, when the beta value was such as negative, for instance, with a value of -0.691789, it would be 0.5068, which means that for an increase of one unit within X, the chance of getting y=1 is just half as likely, which means it is not a positive relationship with the dependent and independent variables.
Do Probability and high odds ratio are identical?
It is easy to get confused between Odds Ratio and Probability However, but there is a distinct distinction.
Let’s take the ‘Income’ and “Response data in which responses are dependent variables, and the value y=1 means “Request for the acceptance of credit cards. This data is input to the software for statistical analysis and using the Logistic Regression model, we determine the A and B values and use them as inputs into the function logit (to be explained below). It can give probabilities of Y=1 for various values of income (the independent/x variables).
Let’s suppose that in output, we discover in the output that the variable (a) (a) is -9.21, and its coefficient (b) is 0.013529. It is clear that the odds ratio is 1.013621, which means that an increase in income will increase the chances of the result being 1 by 1.013621 times. Then we can utilize the logit function in order to calculate the odds ratio for different amounts of income. For another moment, take a step ahead of ourselves by entering these numbers into the Estimated Regression Equation, which is
P = ea + bx / 1 + ea + BX
For an x of 500, the chance of Y=1 is estimated to be 0.0543463 (5.43%).
If we multiply the value of x with 300 points, the likelihood of Y=1 is 0.7689159 (76.89 percent)
This indicates that with an increment of the number 300, the likelihood of Y=1 increases by 71.46 percent. If we need to determine the odds ratio, we can utilize an odds ratio equation and then input the two probabilities in order of the odds ratio of these two X values.
So, it’s 57.89 percent more likely to obtain Y=1 if you add 300 units of increment in the X variable.
Recognizing that odds ratio and probability are two distinct things is crucial. The likelihood of being accepted by those who earn less is lower, while the likelihood of being accepted by those who have more income is very high, however with every increase of 300 units in income, the probability of being accepted increases by the number of times (57.899) which is for any place in the income range or spectrum. If the income goes up from 801 to 1101, the probability of obtaining the Y=1 number will remain the same, that is 57.899, i.e., 57 times. However, the probability of Y=1 may fluctuate.
It is possible to do some calculations to comprehend this.
It is evident the addition of 300 units increases the chance of having Y=1. However, this time, the probability rises by 22.36 percent instead of 71.46 percent as the value of x increases between 500 and 800. Therefore, the greater the income, the higher the chance of having Y=1. But the odds ratio remains identical (57.899). So the odds ratio remains the same for any interval of equal length in an independent variable. Therefore, a person who has increased their income by 300 will increase the chances of being accepted with a percentage that is 57.899, whatever their beginning income. However, the likelihood that they will be accepted into the program is very low for people with lower incomes at the beginning. Thus, while your odds of being accepted are higher, the odds of being accepted are still low, even with a lower income. Therefore, a huge amount of probabilities could be present even if the odds aren’t that high.
To put it into perspective clearly, the chance of spotting a movie star on the way home and then encountering an alien on your door is extremely minimal; however, the chance of finding an actor is large when compared to the likelihood that you will find an alien, making the odds of locating an actor much greater even though the chance of it being a reality is extremely low.
When we are required to determine the odds ratio using coefficients, what method do we use for formulating coefficients?
In contrast to linear Regression, in which the coefficient can be determined by using a technique known as Ordinary Least Square, where the line that is most fitting is calculated by reducing the residuals squared (or simply, the difference between the actual and predicted data points) In Logistic Regression, the coefficient and constant is determined using a technique called the Maximum Probability Estimate (MLE). MLE utilizes a completely different method to determine the beta and alpha. MLE is more effective than the simpler OLS because we don’t forecast values for Y; however, we can predict probabilities for the dichotomous variable. Because that’s the case, OLS cannot be used as it requires a presumption about the normally distributed residuals. Therefore, we perform an algebraic transformation from the linear equation and make use of MLE to calculate both the coefficient and constant. However, the in-depth discussion of how constant and coefficient values are determined using MLE is not within the topic of this blog, and strongly recommended to conduct your own research on this to give you a notion; maximum Likelihood tries to find the lowest deviation between measured and predicted values. It seeks to identify the best fitting line for linear regression. It also uses statistical software to perform multiple iterations on the backend until the smallest variance is identified (also because it attempts to determine the differences between expected and observed values). It’s on similar lines to Chi-square, which is why when using software to perform logistic regression, words like chi-square and chi-square will be present in the report).
Logit Equation
The dependent variable, in this case, doesn’t follow a Gaussian or Gaussian distribution (explained within the Measures of Shape that there could be various probability distributions); however, it is part of the Bernoulli distribution that has an uncertain probability (P). To explain the meaning of a Bernoulli distribution, a single experiment’s probabilistic distribution results in the binary outcome (0/1, yes/no, etc.). In the example above, when you flip a coin only once (we would like heads to be the outcome), this result will be the Bernoulli distribution with a chance that heads are P and tails being 1-P. The random variable representing the experiment is called a Bernoulli randomly distributed variable.
But, if you flip the coin five times (i.e., runs n independent tests), each trial/experiment has its own probability. Each coin flipping is a Bernoulli trial, and their cumulative sum will result in a binomial distribution with the parameters n and p. Therefore, Bernoulli distribution is an example of Binomial Distribution where n=1 (that is, only one trial) and Binomial Distribution is made up of many independent random variables with, each of which is Bernoulli distributed with a success probability of P. (For only one trial, the binomial distribution is equal to Bernoulli distribution).
With logistic regression, we must determine the probability of the unknown for any mixture of independent variables. In our case, for the value x, a logistic regression model is used to calculate the probability that Y=1. Therefore, it is necessary to connect the dependent variable with the probability (a Bernoulli Distribution) as well as the independent variables with different values. The term logit refers to this link.
In logistic regression, in order to identify the P., the objective is to determine that P (p) is for a unidirectional mixture of independent variables. To connect the linear mixture of variables using the Bernoulli distribution, we require the logit function, which assists in connecting them. This is why it converts the linear mixture of variables that can yield any number of values onto the probability spectrum of the Bernoulli distribution (ranging from 0 to 1).
The function is known as the logistic (logit) purpose is that of the log (natural logarithm) of odds, i.e., ln (P * (1-P). The natural logarithm of odds is known as the logit of probabilities.
The natural log of odds (ln (P + (1-P)) also is equivalent to the linear formula, i.e., that is, the linear equation of an independent variable, which includes a+bx (linear regression equation)
This means that by applying this function, we can obtain a sigmoid curve, and the graph of the log link function can be drawn.
These probabilities are run along the X-axis and run between 0 and 1. it is a curve that is constructed based on the Maximum Likelihood Estimate by which we predict probabilities of different values for the x.
Inverse Logit/ Mean Function
Inverse Logit or Inverse log odds is employed because we require the dependent variable, that is, the chance of being located on the Y-axis (refer to the Linear Regression where the dependent variables were always on the Y-axis) to determine the best Fit Line). In order to run the probabilities on the Y-axis and that they have a sigmoid (S-shaped) function curve, The reverse logit is utilized. When we apply the reverse logit, it offers us probabilities of Y=1 for numbers of x.
logit-1(a) =1 / 1+ e-z
In the formula above, the inverse logit can be found by taking the exponent of something (z). Be aware it is the case that exp (exponential function), which is symbolized by “e,” is actually the opposite of the natural logarithm (ln). Also, don’t mix an exponential symbol (‘e’) with the symbol ‘e’ within the equation of linear regression because it is a reference to residual or error, but when “e” is used to describe an exponential function, it always has an extra scripted value.
The formula above can be written as ez1 + ez
Estimated Regression Equation
The estimated Regression equation gives us with estimated probability ( P). The equation is discovered when we employ the inverse logit function to explain something (z) as the sum of a + bx. This means that we can simply calculate an antilog, i.e., the logit’s exponent function.
The equation can be expressed as follows: these ways
p = ez/ 1 +ez (where z = a + bx)
P is the sum of e logit(P)/ 1 + e logit (P)
p = ea +bx/ 1 + ea + BX
The above equation/s ensure that the probabilities are run along the Y-axis. Give the (sigmoid) (S-shaped) function curve that is used to predict probabilities for 1 for Y.
Multiple Logistic Regression
Suppose, If there is more than one independent variable, then the equation is characterized by multiple coefficients (just as it was when using linear regression) and can be described as
ea + b1x1 + . . . bnxn / 1 + ea + b1x1 + b2x2 . . . bnxn
When we use multiple logistic regression, you don’t get a line. Instead, we get a wave since we’re in the 3-dimensional space (i.e., when we have two independent variables). The graph will look like this:
So, logistic regression could be utilized in cases where your dependent variables are dual. In this case, the linear regression formula is converted into an algebraic equation, and probabilities are used to determine whether Y is one or zero; however, it depends on the probability’s cut-off, as the standard cut-off value is 50%. Therefore any linear combination that has a probability of greater than 0.5 is known as Y=1, and less than 0.5 is regarded as Y=0. The cut-off has to be altered. The methods used to evaluate a logistic regression are different from linear because there is no data for R 2. All such aspects related to evaluating the model have been explored in the Evaluation-Classification Models. Since we are working here with a binomial distribution (dependent variable), we need to choose a link function which is best suited for this distribution. It will be the Logit Function. In the above equations, the parameters are selected to maximize the chance of observing the samples instead of making the most of the error sum (like in normal regression). Logistic Regression has become the widely used method to solve classification and provides satisfactory results even when compared with more sophisticated methods like SVM, ANN and others.
