Wrapper Methods is an automated process of reducing features that require no human involvement. We construct a model. Based on its output, a second model is built by choosing features until the right feature set is identified with the greatest accuracy. This is why it selects features at each stage of building a model and selects features until it acquires the highest level of accuracy. Many predictive models are utilized to determine the score of feature subsets using coefficients, the error rate of the model, and other statistics like R-square, t-stats, AIC, and so on.
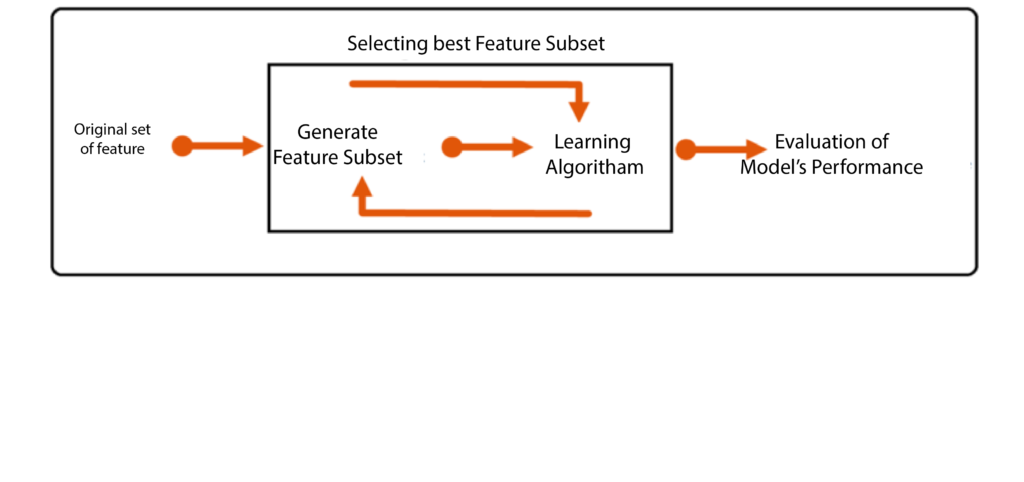
Types of Wrapper Methods
Two kinds of embedded methods exist Stepwise Regression and Recursive feature elimination.
Stepwise Regression
In the Stepwise method, all available independent variables are considered, and the regression model is constructed by removing or adding features according to various parameters. Stepwise methods can be classified into forward selection, Backward Elimination, and Standard Stepwise Regression.
Enter Method
You must be aware of Enter Method earlier to discuss Stepwise Regression, which will assist us in understanding the steps involved in stepwise.
For instance, there is a data set that has 40 features. There is a regression issue, and we decide to use linear regression and then select the features using the Enter Method. We choose all 40 features in this case and then run a linear regression. The model will produce an output where the features’ regression coefficient, p-value, and VIF are listed. Then, we begin to eliminate the features one by one, or even several features at a time, and run the model again to determine whether the model’s accuracy has declined substantially. We remove those features when the p-value is large, meaning they have an insignificant connection with dependent variables.
To address the issue of multicollinearity, we must consider VIF as well, which is also the Variance Inflation Factor which generally indicates the relation that a feature shares in relation to the other variables. In the ideal scenario, variables with VIF=1 should be considered to ensure that all variables have a common underlying, which reduces the possibility of multicollinearity; however, this isn’t feasible since if a variable is related to B and A, then there is a relationship between A and B as well. Thus, the threshold is 2. (for Risk Modelling and Risk Analysis and Clinical Trials) or 3-4 (for Marketing and Sales Analysis).
Therefore, we remove variables with high VIF or p-value; for instance, if we have one with a high p-value and VIF, then we can build the correlation matrix and examine all variables in a relationship to this variable. From this set of correlated variables, we can choose the best number of variables that could be selected after reviewing their respective p-value and VIF. Additionally, domain knowledge is crucial here since certain extremely important variables in real life might have a high p-value or VIF. Still, they might need to be included within the models.
In this process, the model’s accuracy can be continuously monitored. If any feature significantly improves accuracy, the feature should be ignored in the absence of our specified parameters, namely the p-value and the VIF. Therefore, after running several iterations, we need models that have high accuracy (in the case of linear regression models- an R-square that is high with its variation with adjusted R square within the permissible limits of 1 to 22%.) It also has all the necessary variables (all the variables have a p-value below 0.05). It has the minimum amount of multicollinearity (VIF within the limit of 1 to 4).
Enter method is feasible in the case of a small dataset with a few attributes; however, when the data is massive, it can be a difficult task and calls an automated method, and that’s why Stepwise Regression is a great tool.
Forward Selection
The Forward Selection method is a seldom utilized method in which we add features in each stage of the modelling process. It starts with no features included in the model. We then add the features one by one at go and determine if it’s significant or not. If not, then the variable is eliminated. Still, if it is not significant, it is retained while the next feature is added. Its importance is assessed similarly, and so on until all features in the model have reached a significant amount of, for instance, 95 percent. For the model’s accuracy, the model keeps adding the feature when they contribute to improving the precision of the model. It ceases when an additional feature is not contributing to the model’s accuracy. This method has the drawback of not considering the collinear and multicollinear aspects, which could be significant for the dependent variable. These features could enhance the accuracy of the model being trained but can also cause overfitting problems when the model cannot meet the test data. Compared to the entry Method in this method, the VIF is not considered, and the choice is made by p-value and R-square. Additionally, if a particular element is initially entered, but when it is combined with other variables leads to an increase in the accuracy of the model or becomes irrelevant, the feature can’t be eliminated.
Backward Elimination
With Backward Elimination, all the features are added. In each round, the feature that is least important is eliminated. The process continues until all features that are not significant are eliminated. The degree of significance can be determined when the significance level is set to 95%, and the result will contain only the ones with p-values lower than 0.05. Any insignificant variable can decrease or improve the model’s accuracy, and the iterations will be stopped if no significant improvement can be observed in the model’s accuracy due to eliminating the variable. The biggest drawback to the Backward Elimination method is exposure when a variable is removed initially, but is later deemed significant (due to the combination of factors) and can contribute to the model’s accuracy. In the circumstances like this, the feature is removed completely. Furthermore, VIF has not been considered. Therefore, it is not able to address the issue of multicollinearity.
Standard Stepwise Regression
This is majorly employed Wrapper method of deciding on features. In every step, the features are added and taken out in accordance with the improvement in R-square. This acts as a mix of Backward Selection and Forward Elimination. Because variables are continually added and removed based on the accuracy of the model, the issue of multicollinearity can be solved to some extent. Most of the time, Enter Method or Standard Stepwise Regression yield similar results, but they can differ when the data is small. In the case of such situations, the loss of a variable is most likely when Standard Stepwise Regression is employed. Still, if the databases are sufficiently large, both will produce the same results.
This is because, with the use of Stepwise Regression, we can enhance the power of prediction of a model using the least number of predictor variables, making the model impervious to overfitting.
Recursive Feature Elimination
With the method of the Recursive feature, elimination models are built repeatedly. They could be regression or machine-learning models like Support Vector Machine, K Nearest Neighbours, etc. The most effective or worst performing features are selected and put aside whenever a model is constructed. The basis for this performance is usually the coefficient of the feature. This process repeats using the features left and stops when no features are left to build a model. All of these features are eventually ranked according to the order in which they were eliminated, which gives us an assortment of top-quality features.
One should be aware that this method employs an algorithm of greedy optimization for selecting the most effective features, as it makes the decision of choosing features each time according to what is most effective at the particular moment or stage of the process, hoping to eventually determine the subset of most useful features.
Additionally, it should be noted that it’s an extremely unstable technique since it is built upon other models and heavily depends on the kind of model that is used to determine the rank of the attributes. To overcome this Recursive feature elimination must be built on top of other algorithms for modeling and selection which can also be used to use regularization techniques, such as Ridge regression. This means that these models need to be used in the construction of the model to improve the Recursive feature elimination process more stable, providing us with stable and improved results.
Other Methods
Stability Selection
This algorithm was selected in the same way as we did for Recursive Feature Elimination. This time, however, the algorithm is not applied to all data but to different parts of the data with different subsets of features. The process is repeated several times, and the results for each feature are presented. This outcome depends on the number of instances a feature was chosen in the different variations (if it was chosen in the process). The information collected provides us with an understanding of the most crucial features. There is a possibility that something similar could be achieved using different methods. Let’s look at it in comparison to an extremely well-known method for feature reduction, principal Component Analysis. PCA cannot give us reliable estimates of the direction of the maximum variance if there are many features but fewer data in a set of data. In this case, an approach like Stability Selection is an option since it integrates feature selection algorithms with sub-sampling strategies to provide us with stable variables.
There are a variety of wrapper techniques that you can select from. Still, the most simple and popular techniques are the Standard Stepwise method and Recursive Method of Feature Elimination because they are both good automated methods that consider all the aspects that are considered when choosing features (as illustrated in the enter method). Wrapper methods are far quicker and more efficient than filter methods. Another feature reduction technique is embedded methods, which will be discussed in the following blog.
