Feature Transformation is the process of replacing a variable with an operation, which usually aids in the transformation of complex relationships that may be non-linear into linear relationships. It can also help transform the distributions that are not normal, into normal distributions. Different methods of transformation are used to get the mentioned outcomes.
Scenarios for using Transformations
Features must be changed in certain situations, such as the following scenarios:
Non-Linear Relationships
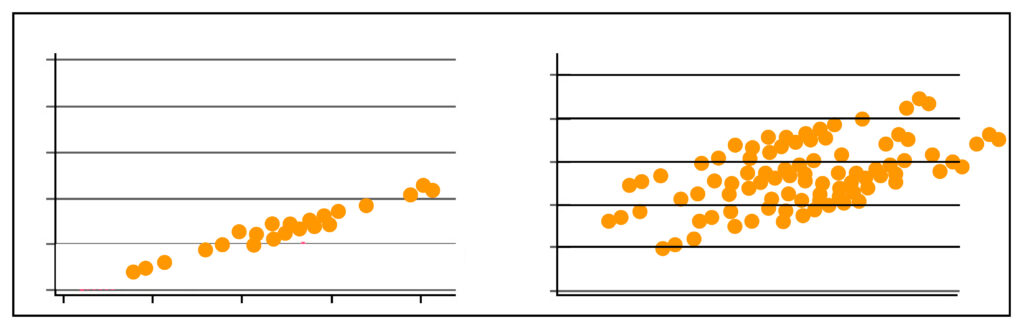
Suppose we employ the Scatterplot to determine the relation of two constant variables and discover that they do not have the same linear relationship. In that case, Transformations are commonly used as it is a method that alters relationships or distributions between a variable and others, usually improving prediction. The Log Transforms can be described as the frequent transforms used in this. Managing income and sales data is a typical scenario where these transformations are required.

Skewed Data
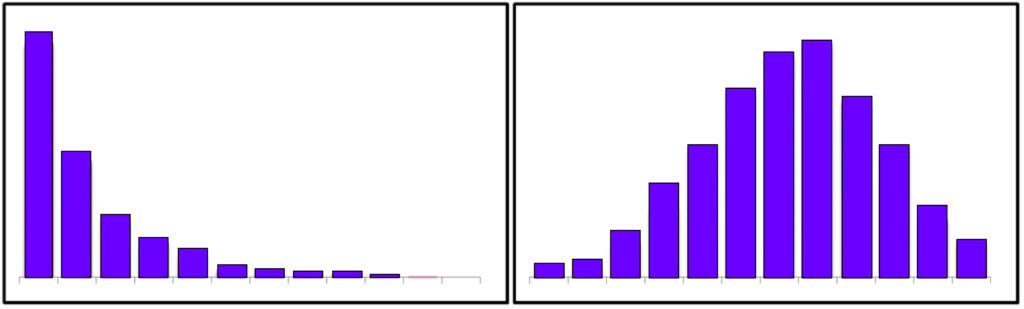
Data may appear distorted due to various reasons, such as extreme outliers (as described in Measures of Shape). Skewed data may create problems for many parametric tests in statistics; the assumption behind them is that the data is generally distributed. If it is a feature of transformation, for example, using log transformations. An irregular distribution could be adjusted to conform by shifting the distribution part more normal and making the data conform to the assumption more closely. This helps in identifying trends in data. The positively skewed distributions could cause data to conform to the normal distribution by applying square/cube root or log transformations.
On the other hand, negatively skewed distributions could be transformed into normal distributions by using the square/cube or exponential of variables. For instance, log-transformation is extensively employed in biomedical, biological, and psycho-social studies to address skewed data because some biological variables don’t conform to the criteria that they are normally distributed or have standard deviations that are homogeneous as required by various parametric tests of statistical significance. Transformations also aid in reducing the impact of outliers and are a great way to deal with outliers.
Methods of Feature Transformation
As we have mentioned, there are many ways to transform features, each with its unique strengths and instances in which they could be used to the maximum advantage. These transforms are substituting a variable with an operation, for instance, replacing a variable named ‘Sales’ with a logarithm or a square/cube root. The different methods of transformation are shown below.
Logarithm
It is among the most popular techniques of transformation. The procedure involves taking the natural logarithms of the variable, where the log of every observation is taken, typically reducing the skewness of the variable. If you combine a variety of independent variables, the result will be the log normal. Particular domains of data are extremely dependent on log transformations, for instance, working with biological parameters, which tend to be skewed. Log transformation can help make the distributions normal and often reveal patterns hidden within dense data. Log transformations may also be utilized when the relationship between the data is very close to exponential.
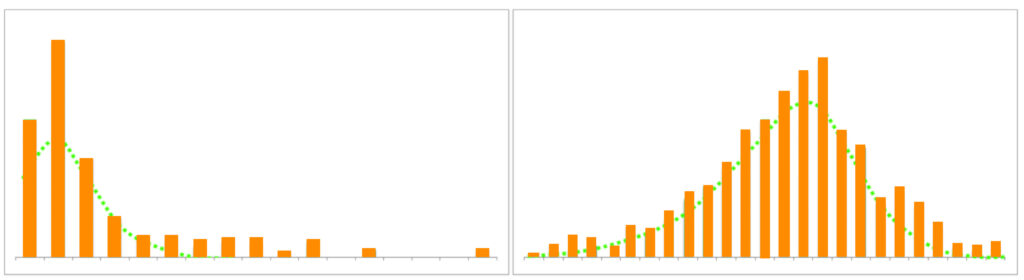
However, it needs to be aware that log transformations can’t be applied to negative or zero values. A constant has to be added to every number to make them non-zero and positive.
Square/Cube Root
The transforming function using Square and Cube root isn’t so popular or important as the logarithmic transformation; it can be utilized when an element is the count of something. The method of transformation involves taking an average of every observation. Then as we make an equal square of the value, the transformation can be applied to negative values, including zero, in contrast to the log.
Arcsine transformation
Also called the arcsine square root transform (or the angular conversion), it is the process of calculating the arcsine from the square root of the number. In certain instances, 2 times the amount of the arcsine of a square root of a percentage is calculated to make the scale of arcsine go between zero and pi; however, if unmultiplied by 2 (Sokal as well as Rohlf 1995) will stop the scale at pi/2. The choice of this method is usually arbitrary. The output is expressed in Radians and ranges from -p/2 up to p/2. Variables ranging between 1 and 0 may be transformed with the help of Arcsine transformation, which can be used to calculate proportions.
Feature Transformation methods offer a fast and simple way to make the data compatible with various types and types of algorithms for modeling. They are especially useful in cases where the data distribution isn’t typical. A variety of Transformation methods were explored in the past and can be utilized according to the kind of data.
